Xác định tọa độ vecto chỉ phương và vecto pháp tuyến

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện :
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.

+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 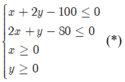
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
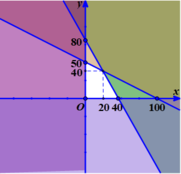
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.


\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{5^2+8^2-7^2}{2.5.8}=\dfrac{1}{2}\)
\(\Rightarrow A=60^0\)

a) Trong mặt phẳng tọa độ, vẽ đường thẳng (�)(d): 2�−�=02x−y=0.
Ta có (�)(d) chia mặt phẳng thành hai nửa mặt phẳng.
Chọn một điểm bất kì không thuộc đường thẳng đó, ví dụ điểm �(1;0)M(1;0). Ta thấy (1;0)(1;0) là nghiệm của bất phương trình đã cho.
Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa bờ (�)(d) và chứa điểm �(1;0)M(1;0) (Miền không được tô màu ở hình vẽ sau).
y x 1 2 O
b) Ta có �−2�2>2�+�+13⇔3(�−2�)−2(2�−�+1)>0⇔−�−4�−2>0⇔�+4�+2<02x−2y>32x+y+1⇔3(x−2y)−2(2x−y+1)>0⇔−x−4y−2>0⇔x+4y+2<0.
Trong mặt phẳng tọa độ, vẽ đường thẳng ΔΔ: �+4�+2=0x+4y+2=0.
Xét điểm �(0;0)O(0;0), thấy (0;0)(0;0) không phải là nghiệm của bất phương trình đã cho do đó miền nghiệm cần tìm là nửa mặt phẳng bờ ΔΔ (không kể đường thẳng ΔΔ) và không chứa điểm �(0;0)O(0;0) (Miền không được tô màu ở hình vẽ sau).
y x 1 − 2 O 1 1 2 −
1.
\(y=3x+1\Leftrightarrow3x-y+1=0\)
d có vtcp là (1;3) và vtpt là (3;-1)
2.
\(y=-\dfrac{1}{2}x\Rightarrow x+2y=0\)
d có vtcp là (2;-1) và vtpt là (1;2)
3.
d có vtcp là (1;0) và vtpt là (0;1)
4.
d có vtcp là (0;1) và vtpt là (1;0)