Giúp mình dới!!!!!!!
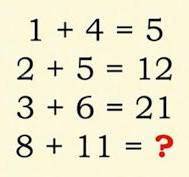
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



khoảng cách là 4,2,2,3,3,2,...
vậy có khả năng số tiếp theo là:17+2=19

1/3 + 1/12 < ? < 1 - 5/12
=>5/12 < ? < 7/12
=>?= 6/12 = 1/2

Bài 9:
a: \(A=\left(\dfrac{1}{3}-\dfrac{8}{15}-\dfrac{1}{7}\right)+\left(\dfrac{2}{3}+\dfrac{-7}{15}+1\dfrac{1}{7}\right)\)
\(=\dfrac{1}{3}-\dfrac{8}{15}-\dfrac{1}{7}+\dfrac{2}{3}+\dfrac{-7}{15}+\dfrac{8}{7}\)
\(=\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\left(-\dfrac{8}{15}-\dfrac{7}{15}\right)+\left(-\dfrac{1}{7}+\dfrac{8}{7}\right)\)
\(=1-1+1=1\)
b: \(B=0,25+\dfrac{3}{5}-\left(\dfrac{1}{8}-\dfrac{2}{5}+1\dfrac{1}{4}\right)\)
\(=0,25+\dfrac{3}{5}-\dfrac{1}{8}+\dfrac{2}{5}-1,25\)
\(=\left(\dfrac{3}{5}+\dfrac{2}{5}\right)+\left(0,25-1,25\right)-\dfrac{1}{8}\)
\(=1-1-\dfrac{1}{8}=-\dfrac{1}{8}\)
c: \(C=\dfrac{3}{4}-\dfrac{4}{5}+\dfrac{5}{6}-\dfrac{6}{7}+\dfrac{7}{8}+\dfrac{6}{7}-\dfrac{5}{6}+\dfrac{4}{5}-\dfrac{3}{4}\)
\(=\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\left(-\dfrac{4}{5}+\dfrac{4}{5}\right)+\left(\dfrac{5}{6}-\dfrac{5}{6}\right)+\left(-\dfrac{6}{7}+\dfrac{6}{7}\right)+\dfrac{7}{8}\)
\(=0+0+0+0+\dfrac{7}{8}=\dfrac{7}{8}\)
d: \(D=\left(2025-\dfrac{5}{181}+\dfrac{1}{50}\right)-\left(4+\dfrac{3}{181}-\dfrac{2}{50}\right)-\left(1-\dfrac{8}{181}+\dfrac{3}{50}\right)\)
\(=2025-\dfrac{5}{181}+\dfrac{1}{50}-4-\dfrac{3}{181}+\dfrac{2}{50}-1+\dfrac{8}{181}-\dfrac{3}{50}\)
\(=2025-4-1=2020\)

Tìm tuổi cô hiện nay hay tìm tuổi cô 3 năm trước em nhỉ?

a: \(\dfrac{-3}{4}+\left(3-\dfrac{1}{4}\right)-\left(2,25-\dfrac{9}{4}\right)\)
\(=-\dfrac{3}{4}+3-\dfrac{1}{4}-\left(2,25-2,25\right)\)
\(=-1+3=2\)
b: \(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{23}+\dfrac{1}{6}\)
\(=\dfrac{1}{2}+\dfrac{1}{6}-\dfrac{1}{3}+\dfrac{1}{23}\)
\(=\dfrac{3+1-2}{6}+\dfrac{1}{23}\)
\(=\dfrac{1}{3}+\dfrac{1}{23}=\dfrac{26}{69}\)
c: \(\left(-\dfrac{13}{7}-\dfrac{4}{9}\right)-\left(-\dfrac{10}{7}-\dfrac{4}{9}\right)\)
\(=-\dfrac{13}{7}-\dfrac{4}{9}+\dfrac{10}{7}+\dfrac{4}{9}\)
\(=-\dfrac{13}{7}+\dfrac{10}{7}=-\dfrac{3}{7}\)
d: \(\dfrac{-14}{12}+0,65-\left(-\dfrac{7}{42}-0,35\right)\)
\(=-\dfrac{7}{6}+0,65+0,35+\dfrac{7}{42}\)
\(=\dfrac{-49}{42}+\dfrac{7}{42}+1=-\dfrac{42}{42}+1=0\)
e: \(\left(\dfrac{7}{8}-\dfrac{5}{2}+\dfrac{4}{7}\right)-\left(-\dfrac{3}{7}+1-\dfrac{13}{8}\right)\)
\(=\dfrac{7}{8}-\dfrac{5}{2}+\dfrac{4}{7}+\dfrac{3}{7}-1+\dfrac{13}{8}\)
\(=\dfrac{20}{8}-\dfrac{5}{2}=\dfrac{5}{2}-\dfrac{5}{2}=0\)
f: \(\dfrac{-3}{7}+\left(3-\dfrac{3}{4}\right)-\left(2,25-\dfrac{10}{7}\right)\)
\(=-\dfrac{3}{7}+2,25-2,25+\dfrac{10}{7}\)
\(=\dfrac{10}{7}-\dfrac{3}{7}=\dfrac{7}{7}=1\)
g: \(\dfrac{1}{2}-\dfrac{43}{101}+\left(-\dfrac{1}{3}\right)-\dfrac{1}{6}\)
\(=\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)-\dfrac{43}{101}\)
\(=\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)-\dfrac{43}{101}=0-\dfrac{43}{101}=-\dfrac{43}{101}\)
h: \(\left(\dfrac{5}{3}-\dfrac{3}{7}+9\right)-\left(2+\dfrac{5}{7}-\dfrac{2}{3}\right)+\left(\dfrac{8}{7}-\dfrac{4}{3}-10\right)\)
\(=\dfrac{5}{3}-\dfrac{3}{7}+9-2-\dfrac{5}{7}+\dfrac{2}{3}+\dfrac{8}{7}-\dfrac{4}{3}-10\)
\(=\left(\dfrac{5}{3}+\dfrac{2}{3}-\dfrac{4}{3}\right)+\left(-\dfrac{3}{7}-\dfrac{5}{7}+\dfrac{8}{7}\right)+\left(9-2-10\right)\)
\(=\dfrac{2}{3}-3=-\dfrac{7}{3}\)
i: \(\dfrac{1}{2}+\dfrac{5}{6}-\dfrac{1}{3}=\dfrac{3}{6}+\dfrac{5}{6}-\dfrac{2}{6}=\dfrac{5+1}{6}=\dfrac{6}{6}=1\)
k: \(\dfrac{1}{2}-\left[\dfrac{3}{8}+\left(-\dfrac{7}{4}\right)\right]\)
\(=\dfrac{1}{2}-\dfrac{3}{8}+\dfrac{7}{4}\)
\(=\dfrac{4}{8}-\dfrac{3}{8}+\dfrac{14}{8}=\dfrac{15}{8}\)

Nửa chu vi mảnh đất ban đầu là 80:2=40(m)
Chiều dài mảnh đất sau khi giảm đi 5m là 40:2=20(m)
Chiều dài mảnh đất là 20+5=25(m)
Chiều rộng mảnh đất là 40-25=15(m)
Diện tích ban đầu là 25x15=375(m2)
Nửa chu vi mảnh đất ban đầu là:
80:2=40(m)
Chiều dài của mảnh đất sau khi giảm đi 5m là:
40 : 2 = 20 (m)
Chiều dài của mảnh đất là:
20 + 5= 25 (m)
Chiều rộng của mảnh đất là:
40 - 25 = 15 (m)
Diện tích ban đầu của mảnh đất là:
25 x 15 = 375 (\(^{m^2}\))
Đáp số:375 \(^{m^2}\)

Lời giải:
$a^2+b^2<2$
$\Leftrightarrow (a-b)^2+2ab<2$
$\Leftrightarrow ab< \frac{2-(a-b)^2}{2}\leq \frac{2}{2}=1$
BĐT cần chứng minh tương đương với:
$\frac{a^2+b^2+2}{(a^2+1)(b^2+1)}\leq \frac{2}{1+ab}$
$\Leftrightarrow (a^2+b^2+2)(1+ab)\leq 2(a^2+1)(b^2+1)$
$\Leftrightarrow a^2+b^2+2+ab(a^2+b^2+2)\leq 2(a^2b^2+a^2+b^2+1)$
$\Leftrightarrow ab(a^2+b^2+2)\leq 2a^2b^2+a^2+b^2$
$\Leftrightarrow ab(a^2+b^2-2ab)-(a^2+b^2-2ab)\leq 0$
$\Leftrightarrow ab(a-b)^2-(a-b)^2\leq 0$
$\Leftrightarrow (a-b)^2(ab-1)\leq 0$ (luôn đúng với mọi $a,b\in\mathbb{R}$ và $ab<1$)
Do đó ta có đpcm.
18
mình nhầm 19