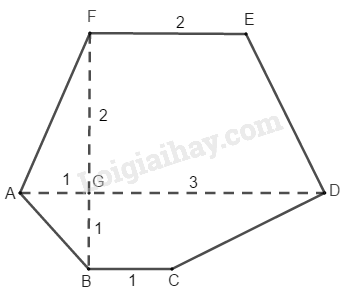
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(x^2+5y^2-4xy-4x+2y+13\)
\(=x^2+4y^2+4-4xy-4x+8y+y^2-6y+9\)
\(=\left(x-2y-2\right)^2+\left(y-3\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x-2y-2=0\\y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=8\\y=3\end{cases}}\)
Suy ra \(M=-1+1=0\)
Chọn A.


Câu 1: Thực hiện:
\(x.\left(x^2-4x\right)=x.x^2-x.4x=x^3-4x^2\)
\(\left(x+1\right).\left(x-4\right)=x^2-4x+x-4=x^2-3x-4\)
Câu 2: Khai triển hằng đẳng thức:
\(\left(2x+1\right)^2=\left(2x\right)^2+2.2x.1+1^2=4x^2+4x+1\)
\(x^3-8=\left(x^2\right)^3-2^3=\left(x-2\right).\left(x^2+x.2+2^2\right)=\left(x-2\right).\left(x^2+2x+4\right)\)
Câu 3: Phân tích đa thức thành nhân tử:
\(2x^2-4x+8=2.\left(x^2-2x+4\right)=2.\left(x-2\right)^2\)
\(12x^2y+12xy+6x+3y+3\)
\(=3.\left(4x^2y+4xy+2x+y+1\right)\)
\(=3.\left(4x^2y+2xy+2xy+2x+y+1\right)\)
\(=3.[\left(4x^2y+2xy+2x\right)+\left(2xy+y+1\right)]\)
\(=3.[2x.\left(2xy+y+1\right)+\left(2xy+y+1\right)]\)
\(=3.\left(2x+1\right).\left(2xy+y+1\right)\)



