a) Xét tam giác AMB và tam giác AMC có:

+ AB = AC (gt).

+ AM chung.

+ ^BAM = ^CAM (AM là phân giác ^BAC).

=> Tam giác AMB = Tam giác AMC (c - g - c).

b) Xét tam giác ABC cân tại A có: AB = AC (gt).

=> Tam giác ABC cân tại A.

Mà AD là phân giác ^BAC (gt).

=> AD là đường trung tuyến (Tính chất các đường trong tam giác cân).

=> D là trung điểm của BC.

Xét tam giác MBD và tam giác MCD có:

+ MB = MC (do tam giác AMB = tam giác AMC).

+ MD chung.

+ BD = CD (do D là trung điểm của BC).

=> Tam giác MBD = Tam giác MCD (c - c - c).

A B C M a. Xét  $\Delta AMB$và $\Delta AMC$

có $\text{⎨}\begin{array}{c}AB=AC\\ \widehat{BAM}=\widehat{CAM}\\ AMchung\end{array}$(do AD là phân giác)$\Rightarrow \Delta AMB=\Delta AMC\left(c-g-c\right)$

$\Rightarrow MB=MC$

b. Xét $\Delta MBD$và $\Delta MCD$

có 
$\{\begin{array}{c}BD=CD\\ MDchung\\ MB=MC\end{array}$$\Rightarrow \Delta MBD=\Delta MCD\left(c-c-c\right)$

A D B C  a) Xét $\Delta CAD$ và $\Delta CBD$, có:

$\begin{array}{c}BC=CA\\ DA=DB\end{array}\}\Rightarrow \Delta CAD=\Delta CDB(c.c.c)$

Vì $\Delta CAD=\Delta CBD\left(cmt\right)$ nên:

$\Rightarrow \widehat{CAD}=\widehat{CBD}$ (2 góc tương ứng)

 b) Vì $\Delta CAD=\Delta CBD\left(cmt\right)$ nên:

$\Rightarrow \widehat{ACD}=\widehat{BCD}$ (2 góc tương ứng)

$\Rightarrow CD$ là phân giác của $\widehat{ACB}$

Có : \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\left(a+b+c\ne0\right)\)

Áp dụng dãy tỉ số bằng nhau, ta có :

\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}=\dfrac{a-b-c}{b-c-d}=1\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b}=1\Rightarrow a=b=1\\\\\dfrac{b}{c}=1\Rightarrow b=c=1\end{matrix}\right.\)

\(\Rightarrow a=b=c\left(đpcm\right)\)

   (2x +1)³ = (2x +1)⁴

  (2x + 1)⁴ - (2x + 1 )³ =0

 (2x + 1)³(2x +1-1) =0

2x(2x+1)³= 0

\(\left[{}\begin{matrix}x=0\\2x+1=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)

   x²(x-7)<0

xét x²(x-7) = 0

⇔ x=0; x = 7

lập bảng xét dấu ta có (có bảng xét dấu kèm theo )

             0 # x < 7 

UUk

B

b.2

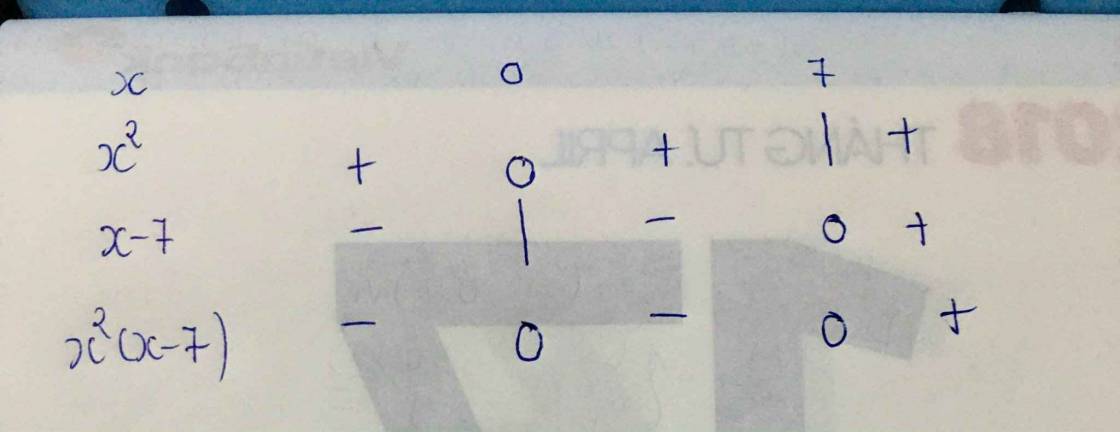
A (đúng):vì mọi số hữu tỉ âm luôn nhỏ hơn số hữu tỉ dương.

B (sai): vì 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.

C (sai): vì tập hợp số nguyên âm là số hữu tỉ âm

D (sai):vì tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0

                           Đáp án là: A