a) Sửa lại đề bài \(xy\left(x+y\right)+yz\left(y+z\right)+zx\left(z+x\right)+3xyz\)

 \(=xy\left(x+y\right)+xyz+yz\left(y+z\right)+xyz+zx\left(z+x\right)++xyz\)

\(=xy\left(x+y+z\right)+yz\left(x+y+z\right)+zx\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left(xy+yz+zx\right)\)

b) Đặt \(t=a-2\Rightarrow\left\{{}\begin{matrix}3t-1=3a-7\\3t+1=3a-5\end{matrix}\right.\)

\(...=t\left(3t-1\right)\left(3t+1\right)-8\)

\(=t\left(9t^2-1\right)-8\)

\(=9t^3-t-8\)

\(=9t^3-9t+8t-8\)

\(=9\left(t^3-1\right)+8\left(t-1\right)\)

\(=9\left(t-1\right)\left(t^2+t+1\right)+8\left(t-1\right)\)

\(=\left(t-1\right)\left[9\left(t^2+t+1\right)+8\right]\)

\(=\left(t-1\right)\left(9t^2+9t+17\right)\)

\(=\left(a-3\right)\left[9\left(a-2\right)^2+9\left(a-2\right)+17\right]\)

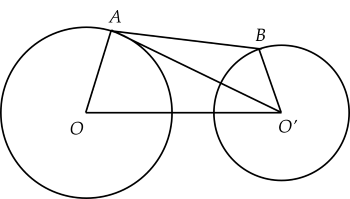
Xét \(\Delta ABO':\)

\(AB\ge O'A-O'B\left(1\right)\)

Xét \(\Delta OAO':\)

\(O'A\ge O'O-OA\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow AB\ge O'O-OA-O'B=950-500-300=150\left(m\right)\)

Dấu '=' xảy ra khi \(4\) điểm \(O;A;B;O'\) thẳng hàng

\(\Rightarrow\) Xây cầu có chiều dài là \(150\left(m\right)\) trên đoạn nối 2 tâm cầu 2 hòn đảo (O'O) thì cây cầu sẽ ngắn nhất.

a: Xét (O) có

MA,MB là các tiếp tuyến

Do đó: MA=MB

=>M nằm trên đường trung trực của AB(1)

Ta có: OA=OB

=>O nằm trên đường trung trực của AB(2)

Từ (1),(2) suy ra OM là đường trung trực của AB

=>OM\(\perp\)AB tại H và H là trung điểm của AB

Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

Xét tứ giác OHBI có \(\widehat{OHB}=\widehat{OIB}=\widehat{HBI}=90^0\)

nên OHBI là hình chữ nhật

b: ΔOBD cân tại O

mà OI là đường cao

nên OI là phân giác của góc BOD

Xét ΔODK và ΔOBK có

OD=OB

\(\widehat{DOK}=\widehat{BOK}\)

OK chung

Do đó: ΔODK=ΔOBK

=>\(\widehat{ODK}=\widehat{OBK}\)

=>\(\widehat{ODK}=90^0\)

=>KD là tiếp tuyến của (O)

c: Xét ΔOBM vuông tại B có BH là đường cao

nên \(OH\cdot OM=OB^2\)

=>\(OH=\dfrac{R^2}{2R}=\dfrac{R}{2}\)

ΔOHB vuông tại H

=>\(OH^2+BH^2=OB^2\)

=>\(BH=\sqrt{R^2-\left(\dfrac{R}{2}\right)^2}=\dfrac{R\sqrt{3}}{2}\)

mà BH=OI

nên \(OI=\dfrac{R\sqrt{3}}{2}\)

ΔOBD cân tại O

mà OI là đường cao

nên I là trung điểm của BD

Ta có: OH=BI

mà BI=ID(I là trung điểm của BD)

nên OH=DI

=>DI=R/2

Xét ΔODK vuông tại D có DI là đường cao

nên \(\dfrac{1}{DI^2}=\dfrac{1}{DO^2}+\dfrac{1}{DK^2}\)

=>\(\dfrac{1}{DK^2}=\dfrac{1}{\left(\dfrac{R}{2}\right)^2}-\dfrac{1}{R^2}=\dfrac{1}{\dfrac{R^2}{4}}-\dfrac{1}{R^2}=\dfrac{3}{R^2}\)

=>\(DK=\dfrac{R\sqrt{3}}{3}\)

ΔADK vuông tại D

=>\(DA^2+DK^2=AK^2\)

=>\(AK=\sqrt{\left(\dfrac{R\sqrt{3}}{3}\right)^2+\left(2R\right)^2}=\dfrac{R\sqrt{39}}{3}\)

Chu vi tam giác ADK là:

AD+DK+AK

\(=2R+\dfrac{R\sqrt{3}}{3}+\dfrac{R\sqrt{39}}{3}=R\left(2+\dfrac{\sqrt{3}+\sqrt{39}}{3}\right)\)

Gọi giá niêm yết của một cái bàn là là x(nghìn đồng)

(Điều kiện: x>0)

Giá niêm yết của một cái quạt điện là 850-x(nghìn đồng)

Giá tiền thực tế của cái bàn là là: \(x\left(1-10\%\right)=0,9x\left(nghìnđồng\right)\)

Giá tiền thực tế của cái quạt điện là:

\(\left(850-x\right)\left(1-20\%\right)=0,8\left(850-x\right)=680-0,8x\left(nghìnđồng\right)\)

Tổng số tiền phải trả là:

850-125=725(nghìn đồng)

=>0,9x+680-0,8x=725

=>0,1x=725-680=45

=>x=450(nhận)

Vậy: Số tiền thực tế anh Bình phải trả cho cái bàn là là: \(450\cdot0,9=405\) nghìn đồng

Số tiền thực tế anh Bình phải trả cho cái quạt điện là:

\(680-0,8\cdot450=320\left(nghìnđồng\right)\)

1: \(A=\sqrt{28}+\sqrt{63}-5\sqrt{8-2\sqrt{7}}\)

\(=2\sqrt{7}+3\sqrt{7}-5\sqrt{\left(\sqrt{7}-1\right)^2}\)

\(=5\sqrt{7}-5\left(\sqrt{7}-1\right)=5\)

2: a: Thay x=25 vào A, ta được:

\(A=\dfrac{5}{5+2}=\dfrac{5}{7}\)

b: \(B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2-\sqrt{x}}\)

\(=\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\)

\(=\dfrac{x+\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)

c: \(P=A:B=\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

\(\sqrt{P}< \dfrac{1}{2}\)

=>\(\left\{{}\begin{matrix}P>=0\\P< \dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+2}-\dfrac{1}{4}< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{4\left(\sqrt{x}-2\right)-\sqrt{x}-2}{4\left(\sqrt{x}+2\right)}< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\4\sqrt{x}-8-\sqrt{x}-2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=4\\3\sqrt{x}< 10\end{matrix}\right.\)

=>\(4< =x< \dfrac{100}{9}\)

Kết hợp ĐKXĐ, ta được: \(4< x< \dfrac{100}{9}\)

mà x là số nguyên nhỏ nhất thỏa mãn

nên x=5

   321 x 2 - 1000

= 642 - 1000

= - 358

Tình yêu vốn dĩ là điều kỳ diệu và tuyệt vời của tạo hóa tuy nhiên là yêu ai, yêu khi nào, yêu ra sao lại là cả một quá trình để trưởng thành. Có lẽ lớp 9 đang là giai đoạn bước ngoặt quan trọng trong cuộc đời của mỗi con người, vì vậy có thể chưa nhất thiết phải yêu đương trong giai đoạn này. Vì vấn đề cấp bách của hiện tại chính là con đường tương lai chông gai phía trước. Nếu ta không thể đủ nội lực và tiềm lực trong tương lai để tự lập thì lúc đó mọi thứ tình yêu đều là xa xỉ, vì thật khó mà có thể tiếp cận với một người mà tương lai của bản thân đã đang quá nhạt mờ. 

Rút gọn phân thức:

A = \(\dfrac{x^4-y^4}{y^3-x^3}\) (đk \(x\ne y\)

A = \(\dfrac{\left(x^2-y^2\right).\left(x^2+y^2\right)}{\left(y-x\right).\left(x^2+xy+y^2\right)}\)

A = \(\dfrac{-\left(y-x\right)\left(x+y\right)\left(x^2+y^2\right)}{\left(y-x\right).\left(x^2+xy+y^2\right)}\)

A = \(\dfrac{-\left(x+y\right).\left(x^2+y^2\right)}{x^2+xy+y^2}\) 

B = \(\dfrac{\left(2x-4\right)\left(x-3\right)}{\left(x-2\right)\left(3x^2-27\right)}\) (đk \(x\) ≠ -3; 2; 3)

B = \(\dfrac{2.\left(x-4\right)\left(x-3\right)}{\left(x-2\right).3.\left(x^2-3^2\right)}\)

B = \(\dfrac{2.\left(x-2\right)\left(x-3\right)}{3.\left(x-2\right)\left(x-3\right)\left(x+3\right)}\)

B = \(\dfrac{2}{3\left(x+3\right)}\)