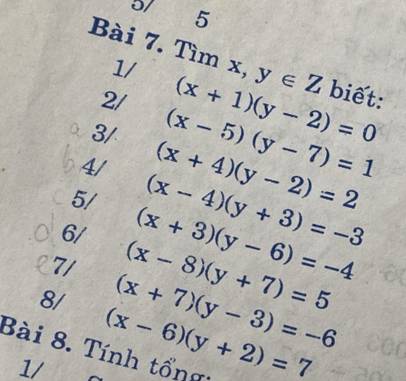
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$S=(3+3^2+3^3+3^4)+(3^5+3^6+3^7+3^8)+....+(3^{97}+3^{98}+3^{99}+3^{100})$
$=3(1+3+3^2+3^3)+3^5(1+3+3^2+3^3)+....+3^{97}(1+3+3^2+3^3)$
$=(1+3+3^2+3^3)(3+3^5+...+3^{97})$
$=40(3+3^5+...+3^{97})$
$=40.3(1+3^4+....+3^{96})$
$=120(1+3^4+...+3^{96})\vdots 120$

Lời giải:
$-1+4-7+10-13+16-...-295+298-301$
$=(-1+4)+(-7+10)+(-13+16)+.....+(-295+298)-301$
$=3+3+3+....+3-301$
Số lần xuất hiện của 3 là: $[(298-1):3+1]:2=50$
$S=3.50-301=-151$

Cho mình xin lỗi nhé , thiếu đk của k . ĐK : k là số tự nhiên

a) -17 < x ≤ 18
⇒ x ϵ {-16;-15;-14;-13;......;13;14;15;16;17;18}
-16 + (-15) + (-14) + (-13) + .... + 13 + 14 + 15 + 16 + 17 + 18
= [-16 + 16] + [(-15) + 15] + [(-14) + 14] + [(-13) + 13] + ... + 17 + 18
= 0 + 0 + 0 + 0 + .... + 17 + 18
= 17 + 18
= 35

7x x 49 = 750
7x x 72 = 750
7x = 750 : 72
7x = 750 - 2
7x = 748
⇒ x = 48

Gọi UWCLN (5n+7;3n+4)=d(dϵN*)
=>(5n+7)⋮d=>3(5n+7)⋮d=>(15n+21)⋮d
=>(3n+4)⋮d=>5(3n+4)⋮d=>(15n+20)⋮d
=>[(25n+21)-(15n+20)]⋮d
=>1⋮d mà dϵN*=>d=1
=>UCLN(5n+7;3n+4)=1
vậy 5n+7 và 3n+4 là 2 số nguyên tố cùng nhau
Chúc bạn học zỏi
Câu 3:
$(x+4)(y-2)=2$
Với $x,y$ nguyên thì $x+4, y-2$ cũng là số nguyên. Mà tích của chúng bằng 2 nên ta có các TH sau:
TH1: $x+4=1, y-2=2\Rightarrow x=-3; y=4$ (thỏa mãn)
TH2: $x+4=-1; y-2=-2\Rightarrow x=-5; y=0$ (thỏa mãn)
TH3: $x+4=2; y-2=1\Rightarrow x=-2; y=3$ (thỏa mãn)
TH4: $x+4=-2; y-2=-1\Rightarrow x=-6; y=1$ (thỏa mãn)
Câu 2:
Với $x,y$ là số nguyên thì $x-5, y-7$ cũng là số nguyên. Mà:
$(x-5)(y-7)=1$ nên ta có các TH sau:
TH1: $x-5=1, y-7=1\Rightarrow x=6; y=8$ (thỏa mãn)
TH2: $x-5=-1; y-7=-1\Rightarrow x=4; y=6$ (thỏa mãn)