Cho ∆ABC nhọn nội tiếp trong đường tròn (O). Các đường cao BE và CF cắt nhau tại H.
a) Chứng minh AEHF là tứ giác nội tiếp.
b) Gọi M và N lần lượt là giao điểm thứ hai của đường tròn (O) với BE và CF. Đường kính AD cắt MN ở I và cắt BE ở K. Chứng minh rằng: KE.KM= KI.KA




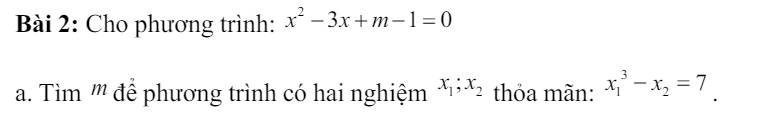
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp