\(\widehat{A}=180^o-\widehat{B}-\widehat{C}=180^o-40^o-40^o=100^o\)

=> \(\widehat{A_{ngoai}}=180^o-100^o=80^o\) 

=> \(\widehat{DAB}=\dfrac{1}{2}\widehat{A_{ngoai}}=\dfrac{1}{2}\cdot80^o=40^o\)

Ta có: \(\widehat{DAB}=\widehat{ABC}\left(=40^o\right)\)

Mà 2 góc này ở vị trí so le trong

=> AD//BC 

cậu giúp mik nhiều ghê, cám ơn nha

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(2\cdot\left(\widehat{OBC}+\widehat{OCB}\right)=90^0\)

=>\(\widehat{OBC}+\widehat{OCB}=45^0\)

Xét ΔOBC có \(\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180^0\)

=>\(\widehat{BOC}+45^0=180^0\)

=>\(\widehat{BOC}=135^0\)

ΔABC cân tại A

=>\(\widehat{BAC}=180^0-2\cdot\widehat{ABC}=100^0\)

AD là phân giác góc ngoài tại đỉnh A

=>\(\widehat{CAD}=\dfrac{180^0-\widehat{BAC}}{2}=40^0\)

=>\(\widehat{CAD}=\widehat{ACB}\left(=40^0\right)\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

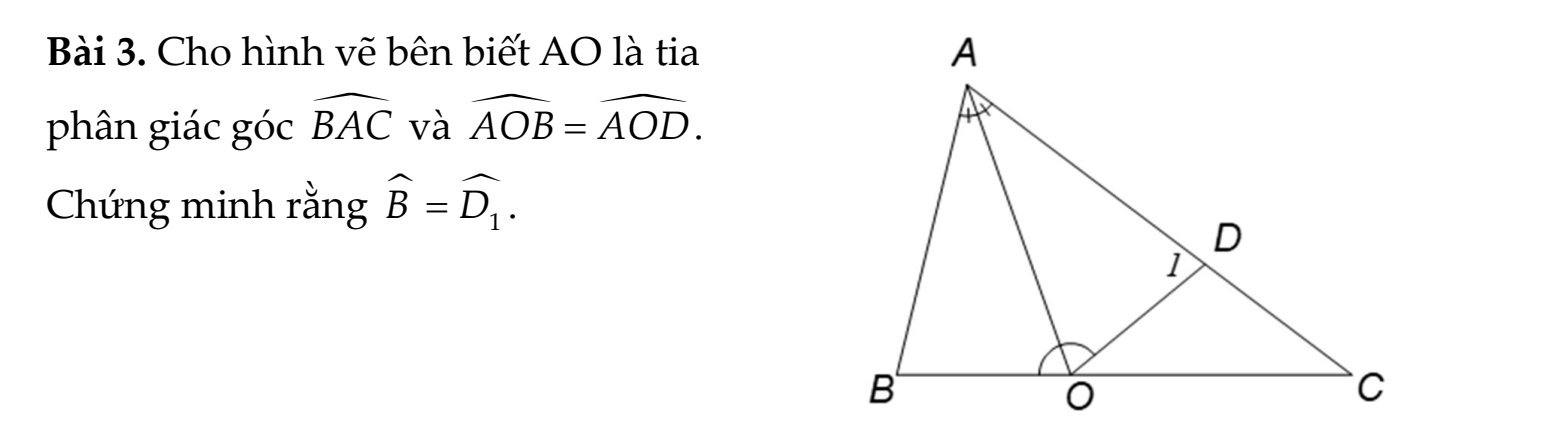
Xét 2 ΔABO và ΔADO ta có:

\(\widehat{BAO}=\widehat{DAO}\) (AD là phân giác của góc BAC) 

\(OA\) chung

\(\widehat{AOB}=\widehat{AOD}\left(gt\right)\) 

\(=>\Delta ABO=\Delta ADO\left(g.c.g\right)\) 

\(=>\widehat{B}=\widehat{D_1}\) (hai góc tương ứng) 

\(2^2+3^2+...+2021^2\)

\(=\left(1^2+2^2+...+2021^2\right)-1\)

\(=\dfrac{2021\cdot\left(2021+1\right)\left(2\cdot2021+1\right)}{6}=1\)

\(=2753594310\)

5:

6:

Bài 5

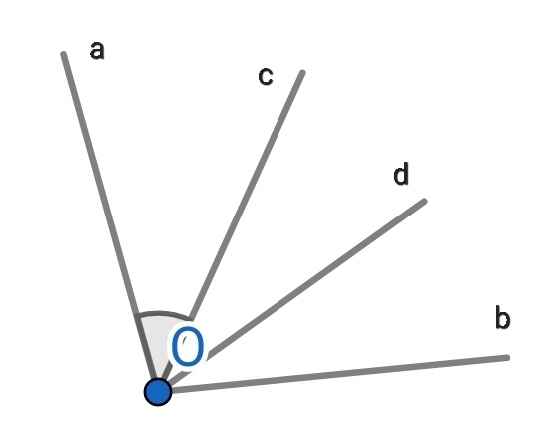
a) Do Oc nằm giữa hai tia Oa và Ob nên

∠aOc + ∠cOb = ∠aOb

⇒ ∠cOb = ∠aOb - ∠aOc

= 100⁰ - 40⁰

= 60⁰

b) Do Od là tia phân giác của ∠cOb (gt)

⇒ ∠cOd = ∠cOb : 2

= 60⁰ : 2

= 30⁰

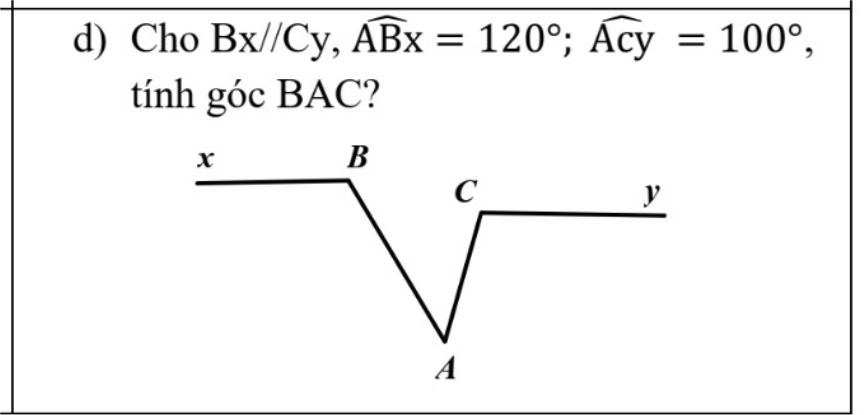
Gọi F là giao điểm của Cy với AB

Bx//Cy

=>\(\widehat{BFC}=\widehat{xBC}\)(hai góc so le trong)

=>\(\widehat{BFC}=120^0\)

Ta có: \(\widehat{BFC}+\widehat{AFC}=180^0\)(hai góc kề bù)

=>\(\widehat{AFC}+120^0=180^0\)

=>\(\widehat{AFC}=60^0\)

Ta có: \(\widehat{ACF}+\widehat{ACy}=180^0\)(hai góc kề bù)

=>\(\widehat{ACF}+100^0=180^0\)

=>\(\widehat{ACF}=80^0\)

Xét ΔACF có \(\widehat{AFC}+\widehat{ACF}+\widehat{CAF}=180^0\)

=>\(\widehat{BAC}=180^0-60^0-80^0=40^0\)

kẻ CM//a và DN//bB(CM và Aa nằm cùng phía với nửa mặt phẳng chứa tia AC, DN và Bb nằm khác phía với nửa mặt phẳng chứa tia DB

CM//Aa

=>\(\widehat{MCA}=\widehat{A_1}\)

Ta có: CM//a

DN//b

mà a//b

nên CM//DN//a//b

CM//DN

=>\(\widehat{MCD}=\widehat{CDN}\)

DN//Bb

=>\(\widehat{NDB}=\widehat{B_1}\)

Ta có: \(\widehat{ACD}=\widehat{ACM}+\widehat{CDM}=\widehat{CDN}+\widehat{B_1}\)

\(\widehat{CDB}=\widehat{CDN}+\widehat{NDB}=\widehat{CDN}+\widehat{B_1}\)

Do đó: \(\widehat{ACD}=\widehat{CDB}\)

Bài 2:

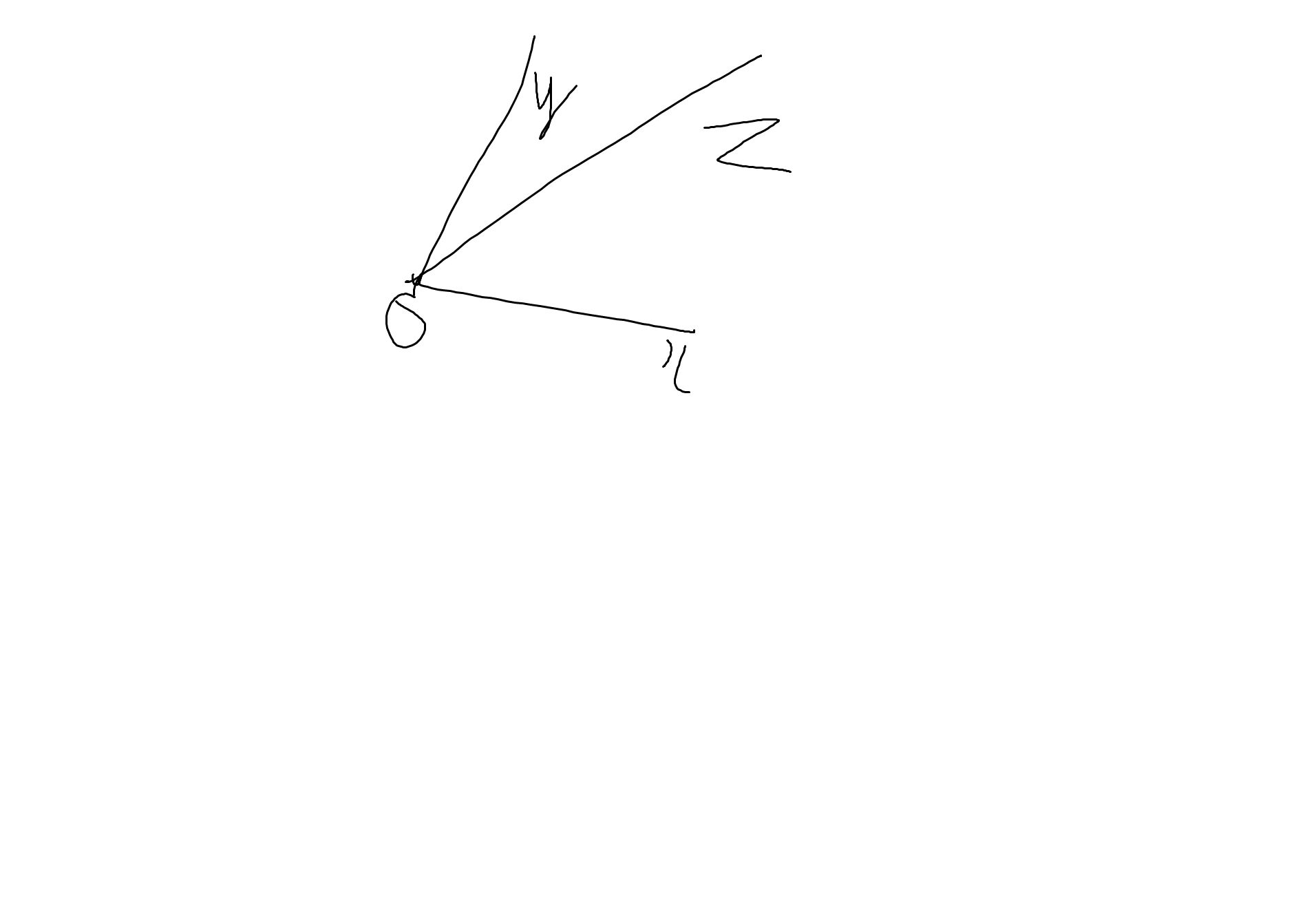
Vì \(\widehat{xOz}< \widehat{xOy}\left(50^0< 80^0\right)\)

nên tia Oz nằm giữa hai tia Ox,Oy

=>\(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)

=>\(\widehat{yOz}=80^0-50^0=30^0\)

Bài 4:

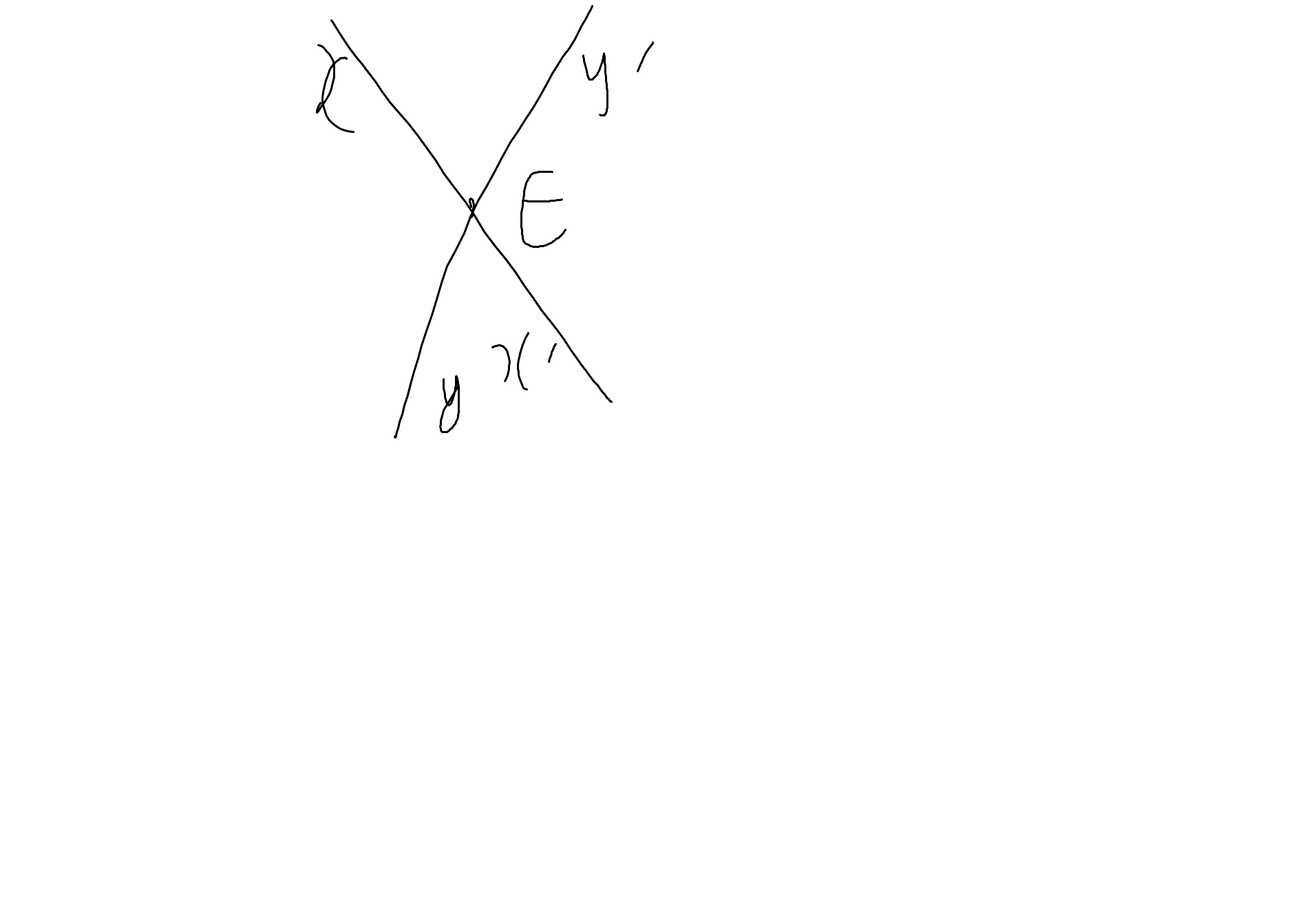
Ta có: \(\widehat{xEy}+\widehat{xEy'}=180^0\)(hai góc kề bù)

=>\(\widehat{xEy'}=180^0-50^0=130^0\)

Ta có: \(\widehat{xEy}=\widehat{x'Ey'}\)(hai góc đối đỉnh)

mà \(\widehat{xEy}=50^0\)

nên \(\widehat{x'Ey'}=50^0\)

Ta có: \(\widehat{xEy'}=\widehat{x'Ey}\)(hai góc đối đỉnh)

mà \(\widehat{xEy'}=130^0\)

nên \(\widehat{x'Ey}=130^0\)

\(\left|x-2\right|>=0\forall x\)

\(\left|2x+y-z\right|>=0\forall x,y,z\)

\(\left|2z+1\right|>=0\forall z\)

Do đó: \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|>=0\forall x,y,z\)

mà \(\left|x-2\right|+\left|2x+y-z\right|+\left|2z+1\right|< =0\)

nên Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\2x+y-z=0\\2z+1=0\\\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\z=-\dfrac{1}{2}\\y=-2x+z=-2\cdot2+\dfrac{-1}{2}=-4-\dfrac{1}{2}=-\dfrac{9}{2}\end{matrix}\right.\)