tìm a,b để x^3+ax+b⋮x^2+x-2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để (d) song song với đường thẳng y=-x+2 thì \(\left\{{}\begin{matrix}m-1=-1\\4\ne2\left(đúng\right)\end{matrix}\right.\)
=>m-1=-1
=>m=0
b: Tọa độ giao điểm của hai đường thẳng y=2x+1 và y=x là:
\(\left\{{}\begin{matrix}2x+1=x\\y=x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=x=-1\end{matrix}\right.\)
Thay x=-1 và y=-1 vào (d), ta được:
\(\left(m-1\right)\cdot\left(-1\right)+4=-1\)
=>-(m-1)=-5
=>m-1=5
=>m=6(nhận)

a: \(\left(a+b\right)=5\)
=>\(\left(a+b\right)^2=5^2=25\)
=>\(a^2+b^2+2ab=25\)
=>\(a^2+b^2=25-2ab=25-2\cdot6=13\)
b: \(\left(a-b\right)^2=a^2+b^2-2ab=13-2\cdot6=1\)
=>\(a-b=\pm1\)
a; (a + b)2 - 2ab
= a2 + 2ab + b2 - 2ab
= a2 + b2 + (2ab - 2ab)
= a2 + b2 + 0
= a2 + b2
vậy a2 + b2 = (a + b)2 - 2ab (1)
Thay a + b = 5 và ab = 6 vào biểu thức (1) ta có:
a2 + b2 = 52 - 2.6 = 25 - 12 = 13
Vậy a2 + b2 = 13

Thay x = 1 và y = 2 vào 2x - y ta có:
\(2\cdot1-2=0\) (1)
THay x = 1 và y= 2 vào 3x - 2y = 11 có:
\(3\cdot1-2\cdot2=-1\) ≠ 11
=> Cặp số (1;2) không phải là nghiệm của hpt: \(\left\{{}\begin{matrix}2x-y=0\\3x-2y=11\end{matrix}\right.\)

a; \(x^3\) + 3\(x^2\) + 3\(x\) + 1
= \(x^3\) + 3\(x^2\).1 + 3\(x\).12 + 13
= (\(x\) + 1)3
b; 27y3 - 9y2 + y - \(\dfrac{1}{27}\)
= (3y)3 - 3(3y)2.\(\dfrac{1}{3}\) + 3.(3y).(\(\dfrac{1}{3}\))2 - (\(\dfrac{1}{3}\))3
= (3y - \(\dfrac{1}{3}\))3

\(A=8abc+4\left(ab+bc+ca\right)+2\left(a+b+c\right)+1\\= 8abc+4ab+4bc+4ca+2a+2b+2c+1\\ =\left(8abc+4ab\right)+\left(4bc+2b\right)+\left(4ca+2a\right)+\left(2c+1\right)\\ =4ab\left(2c+1\right)+2b\left(2c+1\right)+2a\left(2c+1\right)+\left(2c+1\right)\\ =\left(2c+1\right)\left(4ab+2b+2a+1\right)\\ =\left(2c+1\right)\left[\left(4ab+2b\right)+\left(2a+1\right)\right]\\ =\left(2c+1\right)\left[2b\left(2a+1\right)+\left(2a+1\right)\right]\\ =\left(2c+1\right)\left(2a+1\right)\left(2b+1\right)\)

\(A=abc-\left(ab+bc+ca\right)+a+b+c-1\\ =abc-ab-bc-ca+a+b+c-1\\ =\left(abc-ab\right)+\left(-bc+b\right)+\left(-ca+a\right)+\left(c-a\right)\\ =ab\left(c-1\right)-b\left(c-1\right)-a\left(c-1\right)+\left(c-1\right)\\ =\left(ab-b-a+1\right)\left(c-1\right)\\ =\left[b\left(a-1\right)-\left(a-1\right)\right]\left(c-1\right)\\ =\left(a-1\right)\left(b-1\right)\left(c-1\right)\)

Lời giải:
$a^2+b^2=2\Leftrightarrow (a+b)^2=2+2ab=2(ab+1)$
$\Leftrightarrow (a+b)^2=2(a^3+b^3)=2(a+b)(a^2-ab+b^2)$
$\Leftrightarrow (a+b)^2=2(a+b)(2-ab)$
$\Leftrightarrow (a+b)[(a+b)-2(2-ab)]=0$
Nếu $a+b=0$
$\Rightarrow ab+1=a^3+b^3=a^3+(-a)^3=0\Rightarrow ab=-1$
Nếu $a+b-2(2-ab)=0$
$\Leftrightarrow a+b=4-2ab$
$\Rightarrow (a+b)^2=(4-2ab)^2$
$\Leftrightarrow a^2+b^2+2ab=16+4a^2b^2-16ab$
$\Leftrightarrow 2+2ab=16+4a^2b^2-16ab$
$\Leftrightarrow 4a^2b^2-18ab+14=0$
$\Leftrightarrow 2a^2b^2-9ab+7=0$
$\Leftrightarrow (ab-1)(2ab-7)=0$
$\Rightarrow ab=1$ hoặc $ab=\frac{7}{2}$
Thử lại:
Nếu $ab=-1\Rightarrow a^3+b^3=1+ab=0\Rightarrow a=-b$.
$\Rightarrow -1=ab=a.(-a)=-a^2\Rightarrow a^2=1$
$\Rightarrow a=\pm 1\Rightarrow b=\mp 1$
Nếu $ab=1\Rightarrow (a+b)^2=2+2ab=4\Rightarrow a+b=\pm 2$
$a^3+b^3=1+ab=2$
$\Leftrightarrow (a+b)^3-3ab(a+b)=2$
$\Leftrightarrow (a+b)^3-3(a+b)=2$. Thay $a+b=2$ và $a+b=-2$ vào thấy $a+b=2$.
Từ $ab=1, a+b=2\Rightarrow a(2-a)=1$
$\Rightarrow (a-1)^2=0\Rightarrow a=1\Rightarrow b=1$.
Nếu $ab=\frac{7}{2}$:
$(a-b)^2=a^2+b^2-2ab=2-2.\frac{7}{2}=-5<0$ (vô lý - loại)
Vậy $ab=\pm 1$
Với $ab=1$ thì $a=b=1$
Với $ab=-1$ thì $(a,b)=(1,-1)$ hoặc $(a,b)=(-1,1)$

a, Ta có tam giác ABC vuông cân tại A nên ^ABC = ^ACB = 450
Tam giác AEC vuông cân tại E => ^EAC = ^ECA = 450
=> ^BCE = ^BCA + ^ECA = 900
=> BC vuông EC
mà AE vuông EC
=> AE // BC mà ^BCE = ^AEC = 900
Vậy tứ giác AECB là hình thang vuông tại E;C
b, ^BAE = ^BAC + ^EAC = 1350
^ABC = 450
a, Ta có tam giác ABC vuông cân tại A nên ^ABC = ^ACB = 450
Tam giác AEC vuông cân tại E => ^EAC = ^ECA = 450
=> ^BCE = ^BCA + ^ECA = 900
=> BC vuông EC
mà AE vuông EC
=> AE // BC mà ^BCE = ^AEC = 900
Vậy tứ giác AECB là hình thang vuông tại E;C
b, ^BAE = ^BAC + ^EAC = 1350
^ABC = 450

a: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(HB=\sqrt{16^2-12^2}=\sqrt{256-144}=\sqrt{112}=4\sqrt{7}\left(cm\right)\)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(HC=\sqrt{20^2-12^2}=16\left(cm\right)\)
b: Xét ΔDHC có
CA,DE là các đường trung tuyến
CA cắt DE tại F
Do đó: F là trọng tâm của ΔDHC
Xét ΔDHC có
F là trọng tâm
M là trung điểm của CD
Do đó: H,F,M thẳng hàng
c: ΔCHD vuông tại H
mà HM là đường trung tuyến
nên \(HM=\dfrac{1}{2}CD\)
Xét ΔDHC có
HM là đường trung tuyến
F là trọng tâm
Do đó: \(HF=\dfrac{2}{3}HM=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot CD=\dfrac{1}{3}CD\)
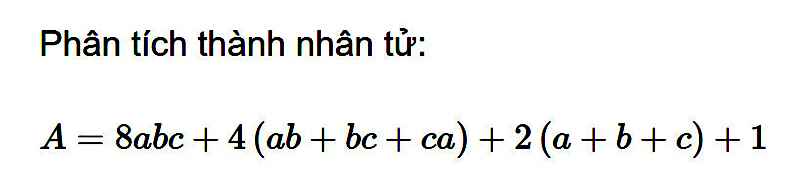
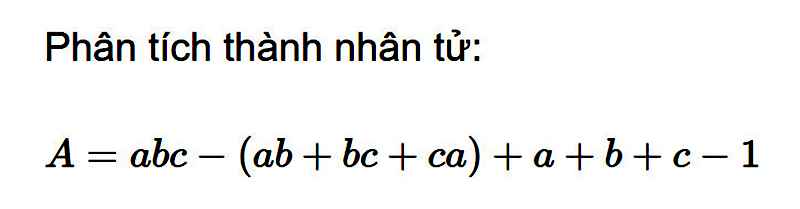
\(x^3+ax+b⋮x^2+x-2\)
=>\(x^3+x^2-2x-x^2-x+2+\left(a+3\right)x+b-2⋮x^2+x-2\)
=>\(\left\{{}\begin{matrix}a+3=0\\b-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)
bạn giải thích bước 1 giùm mình được ko ạ