
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5\cdot\dfrac{5^{37}-1}{5^{38}-1}=\dfrac{5^{38}-5}{5^{38}-1}=1-\dfrac{4}{5^{38}-1}\)
\(\dfrac{5\left(5^{36}+1\right)}{5^{37}+1}=\dfrac{5^{37}+5}{5^{37}+1}=1+\dfrac{4}{5^{37}+1}\)
mà \(-\dfrac{4}{5^{38}-1}< \dfrac{4}{5^{37}+1}\)
nên \(5\cdot\dfrac{5^{37}-1}{5^{38}-1}< 5\cdot\dfrac{5^{36}+1}{5^{37}+1}\)
=>\(\dfrac{5^{37}-1}{5^{38}-1}< \dfrac{5^{36}+1}{5^{37}+1}\)

Gọi tuổi mẹ là x(tuổi)
(Điều kiện: x>0)
Tuổi con là \(\dfrac{3}{5}x\left(tuổi\right)\)
Tuổi mẹ cách đây 9 năm là x-9(tuổi)
Tuổi con cách đây 9 năm là \(\dfrac{3}{5}x-9\left(tuổi\right)\)
Tuổi mẹ gấp đôi tuổi con nên \(x-9=2\left(\dfrac{3}{5}x-9\right)\)
=>\(\dfrac{6}{5}x-18=x-9\)
=>\(\dfrac{1}{5}x=9\)
=>x=45(nhận)
vậy: Tuổi mẹ là 45 tuổi
Tuổi con là \(\dfrac{3}{5}\cdot45=27\left(tuổi\right)\)

\(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4\right)-\left(x^2-16\right)\left(x+4\right)+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4-x-4+3\right)\)
\(=-5\left(x^2-16\right)=-5x^2+80\)

Ta có:
\(\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{y}{4}\\\dfrac{y}{5}=\dfrac{z}{7}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=\dfrac{y}{20}\\\dfrac{y}{20}=\dfrac{z}{28}\end{matrix}\right.\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(2x+3y-z=372\) được:
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{372}{62}=6\)
Suy ra:
\(\left\{{}\begin{matrix}x=15.6=90\\y=20.6=120\\z=28.6=168\end{matrix}\right.\)
Vậy \(x=90;y=120;z=168\)
Ta có \(\dfrac{x}{3}=\dfrac{y}{4}\)và \(\dfrac{y}{5}=\dfrac{z}{7}\)
\(\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)và 2x + 3y - z = 372
Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x+3y-z}{2.15+3.20-28}=6\)
\(\Rightarrow x=90;y=120;z=168\)

Bài 11: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
=>\(\left(2a+13b\right)\left(3c-7d\right)=\left(3a-7b\right)\left(2c+13d\right)\)
=>\(6ac-14ad+39bc-91bd=6ac+39ad-14bc-91bd\)
=>-14ad-39ad=-14bc-39bc
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)
Bài 12:
\(\dfrac{a+2019}{a-2019}=\dfrac{b+2020}{b-2020}\)
=>\(\left(a+2019\right)\left(b-2020\right)=\left(a-2019\right)\left(b+2020\right)\)
=>\(ab-2020a+2019b-2019\cdot2020=ab+2020a-2019b-2019\cdot2020\)
=>-2020a-2020a=-2019b-2019b
=>2020a=2019b
=>\(\dfrac{a}{2019}=\dfrac{b}{2020}\)

Cho số người đội A;B;C lần lượt là a;b;c (a;b;c>0)
Theo bài ra ta có
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)và a + b + c = 130
Theo tc dãy tỉ số bằng nhau
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{130}{9}\)
- bn xem lại đề nhé

a, Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{22}{-2}=-11\Rightarrow x=-33;y=-55\)
b, \(\dfrac{5}{2}=\dfrac{y}{x}\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\Rightarrow x=-6;y=-15\)
c, \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=-\dfrac{21}{-4}=7\Rightarrow x=28;y=49\)

Bài 5: Gọi số người của đội A,đội B,đội C lần lượt là a(người),b(người),c(người)
(Điều kiện: \(a,b,c\in Z^+\))
Tổng số người của ba đội là 130 người nên a+b+c=130
Số cây mỗi người của đội A;B;C trồng được lần lượt là 2;3;4 cây nên 2a=3b=4c
=>\(\dfrac{2a}{12}=\dfrac{3b}{12}=\dfrac{4c}{12}\)
=>\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b+c}{6+4+3}=\dfrac{130}{13}=10\)
=>\(a=10\cdot6=60;b=4\cdot10=40;c=3\cdot10=30\)
Vậy: số người của đội A,đội B,đội C lần lượt là 60(người),40(người),30(người)

Bài 8:
a: \(\dfrac{x}{5}=\dfrac{y}{6}\)
=>\(\dfrac{x}{20}=\dfrac{y}{24}\)
\(\dfrac{y}{8}=\dfrac{z}{7}\)
=>\(\dfrac{y}{24}=\dfrac{z}{21}\)
Do đó: \(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=k\)
=>x=20k;y=24k;z=21k
x+y-z=69
=>20k+24k-21k=69
=>23k=69
=>k=3
=>\(x=20\cdot3=60;y=24\cdot3=72;z=21\cdot3=63\)
b: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
=>x=3k;y=4k;z=5k
\(2x^2+2y^2-3z^2=-100\)
=>\(2\cdot\left(3k\right)^2+2\cdot\left(4k\right)^2-3\cdot\left(5k\right)^2=-100\)
=>\(k^2=4\)
=>\(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
TH1: k=2
=>\(x=3\cdot2=6;y=4\cdot2=8;z=5\cdot2=10\)
TH2: k=-2
=>\(x=3\cdot\left(-2\right)=-6;y=4\cdot\left(-2\right)=-8;z=5\cdot\left(-2\right)=-10\)
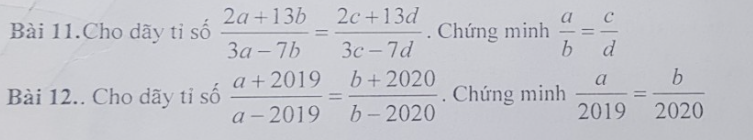

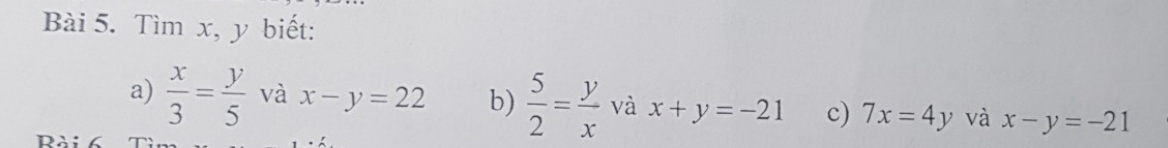

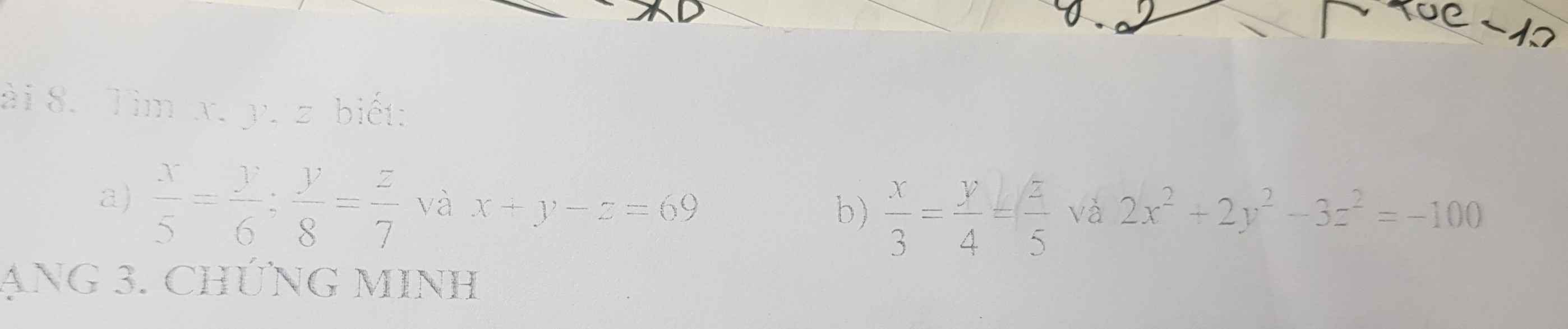
Bài 3:
\(a.-4,36\\ =\dfrac{-436}{100}\\ =\dfrac{-436:4}{100:4}\\ =\dfrac{-109}{25}\\b.0,708\\ =\dfrac{708}{1000}\\ =\dfrac{708:4}{1000:4}\\ =\dfrac{177}{250}\)
Bài 4: \(\dfrac{5}{12}=0,41\left(6\right)\)
\(-\dfrac{8}{11}=-0,\left(72\right)\)
\(\dfrac{3}{22}=0,1\left(36\right)\)
\(-\dfrac{111}{36}=-3,08\left(3\right)\)
Bài 5:
a: \(3,\left(15\right)=3+\dfrac{15}{99}=3+\dfrac{5}{33}=\dfrac{3\cdot33+5}{33}=\dfrac{104}{33}\)
b: \(0,2\left(07\right)=0,2+0,0\left(07\right)=\dfrac{41}{198}\)
c: \(0,1\left(37\right)=0,1+0,0\left(37\right)=\dfrac{1}{10}+\dfrac{37}{990}=\dfrac{68}{495}\)
d: \(0,20\left(23\right)=0,20+0,00\left(23\right)=0,2+\dfrac{23}{9900}=\dfrac{2003}{9900}\)