\(x-\dfrac{1}{1.2}-\dfrac{1}{2.3}-\dfrac{1}{3.4}-...-\dfrac{1}{98.99}=\dfrac{1}{100}+\dfrac{1}{99.100}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$\frac{x+1}{10}+\frac{x+1}{11}+\frac{x+1}{12}=\frac{x+1}{13}+\frac{x+1}{14}$
$\Rightarrow (x+1)(\frac{1}{10}+\frac{1}{11}+\frac{1}{12})=(x+1)(\frac{1}{13}+\frac{1}{14})$
$\Rightarrow (x+1)(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14})=0$
Hiển nhiên $\frac{1}{10}+\frac{1}{11}+\frac{1}{12}-\frac{1}{13}-\frac{1}{14}>0$
$\Rightarrow x+1=0$
$\Rightarrow x=-1$

Lời giải:
Điều kiện: $x\neq -2; x\neq -2; x\neq -8; x\neq -14$
Đề bài
$\Rightarrow \frac{(x+4)-(x+2)}{(x+2)(x+4)}+\frac{(x+8)-(x+4)}{(x+4)(x+8)}+\frac{(x+14)-(x+8)}{(x+8)(x+14)}=\frac{x}{(x+2)(x+14)}$
$\Rightarrow \frac{1}{x+2}-\frac{1}{x+4}+\frac{1}{x+4}-\frac{1}{x+8}+\frac{1}{x+8}-\frac{1}{x+14}=\frac{x}{(x+2)(x+14)}$
$\Rightarrow \frac{1}{x+2}-\frac{1}{x+14}=\frac{x}{(x+2)(x+14)}$
$\Rightarrow \frac{12}{(x+2)(x+14)}=\frac{x}{(x+2)(x+14)}$
$\Rightarrow 12=x$ (thỏa mãn)

Trước tiên ta cần chứng minh : Với a<b thì : \(\dfrac{a}{b}< \dfrac{a+c}{b+c}\) với c là số nguyên dương.
\(\Leftrightarrow a.\left(b+c\right)< b.\left(a+c\right)\)
\(\Leftrightarrow ab+ac< ab+bc\)
\(\Leftrightarrow ac< bc\)
\(\Leftrightarrow a< b\left(LĐ\right)\)
Áp dụng bổ đề đó ta có : \(\dfrac{a}{b+c}< \dfrac{a+a}{a+b+c}=\dfrac{2a}{a+b+c}\)
\(CMTT:\dfrac{b}{c+a}< \dfrac{2b}{a+b+c}\)
\(\dfrac{c}{a+b}< \dfrac{2c}{a+b+c}\)
Do đó : \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< \dfrac{2a+2b+2c}{a+b+c}\)
\(\Rightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< 2\left(đpcm\right)\)
Lời giải:
Vì $b+c> a\Rightarrow 2(b+c)> a+b+c$
$\Rightarrow b+c> \frac{a+b+c}{2}$
$\Rightarrow \frac{a}{b+c}< \frac{2a}{a+b+c}(1)$
Hoàn toàn tương tự ta có:
$\frac{b}{c+a}< \frac{2b}{a+b+c}(2)$
$\frac{c}{a+b}< \frac{2c}{a+b+c}(3)$
Từ $(1); (2); (3)\Rightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< \frac{2(a+b+c)}{a+b+c}=2$
Ta có đpcm.

Tổng A có 1000 số hạng.
�>100110002+1000.1000=1001.10001000(1000+1)=1A>10002+10001001.1000=1000(1000+1)1001.1000=1
�<100110002.1000=10011000=1+11000<2A<100021001.1000=10001001=1+10001<2
Vậy 1<�<2⇒12<�2<22⇒1<�2<41<A<2⇒12<A2<22⇒1<A2<4
Chúc bạn học tốt.
Tổng A có 1000 số hạng
A>(1001/1000^2+1000)*1000=1001*1000/1000*(1000+1)=1
A<(1001/1000^2)*1000=1001/1000=1+1/1000<1
Vậy 1<A<2 nên 1<A^2<4

1 dm3 = 1l nước
Thể tích nước cho phép:
1 . 0,5 . 0,4= 0,2 (m3)
Đổi: 0,2 m3 = 200 dm3
200 dm3 = 200 l nước
Số can nước cần dùng:
200 : 10 = 20 (can)
Vậy cần 20 can nước như vậy để đổ vào bể mực nước cho phép.
Thể tích bể cá là: 1 . 0,5 . 0,4 = 0,2 (m3) = 200l
Cần số can nước là: 200 : 10 = 20 (can)
Vậy cần 20 can nước như vậy đổ vào bể để được mực nước cho phép.

g, 2|\(x+1\)| +(y + \(x\))2 = 0
|\(x\) + 1| ≥ 0 ∀ \(x\)
(y + \(x\))2 ≥ 0 ∀ \(x\); y
⇒2.|\(x\) +1| + (y + \(x\))2 = 0 ⇔ \(\left\{{}\begin{matrix}x+1=0\\y+x=0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
h, -2\(x^3\) + 4\(x\) = 0
2\(x\).( -\(x^2\) + 2) =0
\(\left[{}\begin{matrix}2x=0\\-x^2+2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=\pm\sqrt{2}\end{matrix}\right.\)
Vậy \(x\in\) {-\(\sqrt{2}\); 0; \(\sqrt{2}\)}


\(a,2\left|3x-1\right|+1=5\\ \Rightarrow2\left|3x-1\right|=5-1\\ \Rightarrow2\left|3x-1\right|=4\\ \Rightarrow\left|3x-1\right|=4:2\\ \Rightarrow\left|3x-1\right|=2\\ \Rightarrow\left[{}\begin{matrix}3x-1=2\\3x-1=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x=3\\3x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
\(b,\left|\dfrac{x}{2}-1\right|=3\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}-1=3\\\dfrac{x}{2}-1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}=4\\\dfrac{x}{2}=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-4\end{matrix}\right.\)
\(c,\left|-x+\dfrac{2}{5}\right|+\dfrac{1}{2}=3,5\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3,5-\dfrac{1}{2}\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3\\ \Rightarrow\left[{}\begin{matrix}-x+\dfrac{2}{5}=3\\-x+\dfrac{2}{5}=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}-x=\dfrac{13}{5}\\-x=-\dfrac{17}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{13}{5}\\x=\dfrac{17}{5}\end{matrix}\right.\)
\(d,\left|x-\dfrac{1}{3}\right|=2\dfrac{3}{5}\\ \Rightarrow\left|x-\dfrac{1}{3}\right|=\dfrac{13}{5}\\ \Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{13}{5}\\x-\dfrac{1}{3}=-\dfrac{13}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{13}{5}+\dfrac{1}{3}\\x=-\dfrac{13}{5}+\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{44}{15}\\x=-\dfrac{34}{15}\end{matrix}\right.\)
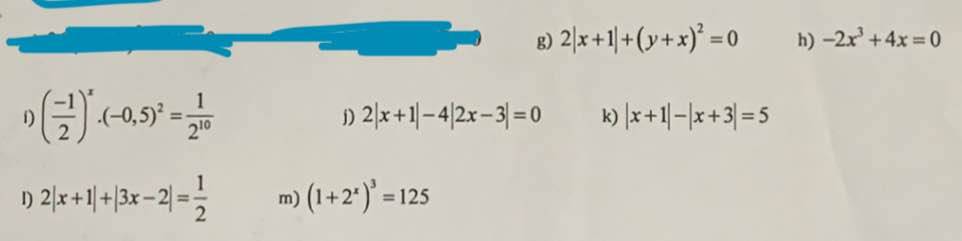

Lời giải:
$x=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{98.99}+\frac{1}{99.100}+\frac{1}{100}$
$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{99-98}{98.99}+\frac{100-99}{99.100}+\frac{1}{100}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}+\frac{1}{100}$
$=1$
`# \text {DNamNgV}`
\(x-\dfrac{1}{1\cdot2}-\dfrac{1}{2\cdot3}-\dfrac{1}{3\cdot4}-...-\dfrac{1}{98\cdot99}=\dfrac{1}{100}+\dfrac{1}{99\cdot100}\)
\(\Rightarrow x-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{98\cdot99}\right)=\dfrac{1}{100}+\dfrac{1}{99}-\dfrac{1}{100}\)
\(\Rightarrow x-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{98}-\dfrac{1}{99}\right)=\dfrac{1}{99}\)
\(\Rightarrow x-\left(1-\dfrac{1}{99}\right)=\dfrac{1}{99}\)
\(\Rightarrow x-\dfrac{98}{99}=\dfrac{1}{99}\)
\(\Rightarrow x=\dfrac{1}{99}+\dfrac{98}{99}\)
\(\Rightarrow x=\dfrac{99}{99}\)
\(\Rightarrow x=1\)
Vậy, `x = 1.`