\(\dfrac{1}{7}\left(\dfrac{7}{3.10}+\dfrac{7}{10.17}+...+\dfrac{7}{73.80}-\left(\dfrac{7}{2.9}+\dfrac{7}{9.16}+...+\dfrac{7}{23.30}\right)\right)\)

\(=\dfrac{1}{7}\left(\dfrac{1}{3}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{17}+...+\dfrac{1}{73}-\dfrac{1}{80}-\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{23}-\dfrac{1}{30}\right)\right)\)

\(=\dfrac{1}{7}\left(\dfrac{1}{3}-\dfrac{1}{80}-\left(\dfrac{1}{2}-\dfrac{1}{30}\right)\right)\)

\(=\dfrac{1}{7}\left(\dfrac{77}{240}-\dfrac{7}{15}\right)=\dfrac{1}{7}.\left(-\dfrac{7}{48}\right)=-\dfrac{1}{48}\)

dỗiii c-các cậu vì ko lm hộ t-tớ -((

\(-2x^2=-32\)

\(\Rightarrow x^2=\dfrac{-32}{-2}\)

\(\Rightarrow x^2=16\)

\(\Rightarrow x^2=4^2\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

Vậy: ... 

\(\left(3-\dfrac{1}{4}+\dfrac{2}{3}\right)-\left(5-\dfrac{1}{3}-\dfrac{6}{5}\right)-\left(6-\dfrac{7}{4}+\dfrac{3}{2}\right)\)

\(=3-\dfrac{1}{4}+\dfrac{2}{3}-5+\dfrac{1}{3}+\dfrac{6}{5}-6+\dfrac{7}{4}-\dfrac{3}{2}\)

\(=\left(3-5-6\right)-\left(\dfrac{1}{4}-\dfrac{7}{4}\right)-\dfrac{3}{2}+\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\dfrac{6}{5}\)

\(=-8-\dfrac{6}{4}-\dfrac{3}{2}+\dfrac{3}{3}+\dfrac{6}{5}\)

\(=-8-\dfrac{3}{2}-\dfrac{3}{2}+1+\dfrac{6}{5}\)

\(=-7-3+\dfrac{6}{5}\)

\(=\dfrac{6}{5}-10\)

\(=-\dfrac{44}{5}\)

Để A = 0 thì |x² - 1| = 0 và |x + 1| = 0

*) |x² - 1| = 0

x² - 1 = 0

x² = 1

x = 1 hoặc x = -1 (1)

*) |x + 1| = 0

x + 1 = 0

x = -1 (2)

Từ (1) và (2) ⇒ x = -1

Vậy x = -1 thì A = 0

Bạn xem lại nhé mình trả lời rồi nha bạn không nên đăng lại nhé ! 

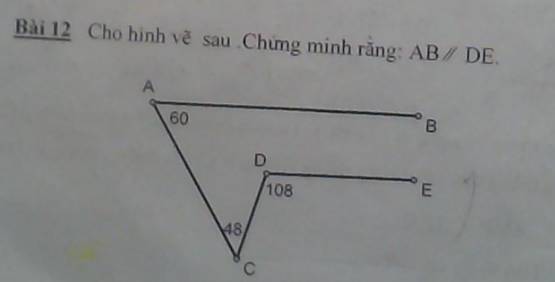
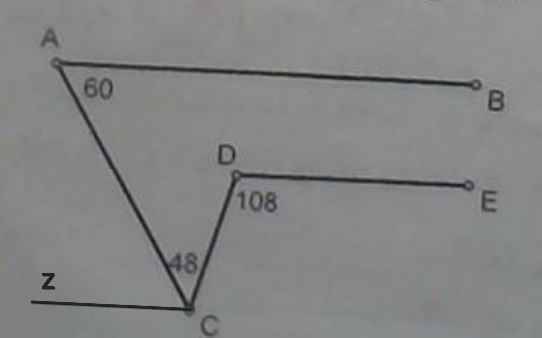  Qua C vẽ tia Cz // DE

⇒ ∠DCz = ∠CDE = 108⁰

⇒ ∠zCA = ∠DCz - ∠DCA

= 108⁰ - 48⁰

= 60⁰

⇒ ∠zCA = ∠CAB = 60⁰

Mà ∠zCA và ∠CAB là hai góc so le trong

⇒ Cz // AB

Lại có:

Cz // DE

⇒ AB // DE

\(\dfrac{-3}{4}< \dfrac{a}{12}< \dfrac{-5}{9}\)

\(\Rightarrow\dfrac{-27}{36}< \dfrac{3a}{36}< \dfrac{-20}{36}\)

\(\Rightarrow-27< 3a< -20\)

\(\Rightarrow a=\left\{-8;-7\right\}\)

\(\dfrac{1}{1-\dfrac{1}{1-2^{-1}}}+\dfrac{1}{1+\dfrac{1}{2^{-1}}}\)

\(=\dfrac{1+\dfrac{1}{2^{-1}}+1-\dfrac{1}{2^{-1}}}{\left(1-\dfrac{1}{2^{-1}}\right)\left(1+\dfrac{1}{2^{-1}}\right)}\)

\(=\dfrac{2}{\left(1-2\right)\left(1+2\right)}=\dfrac{2}{1-4}=-\dfrac{2}{3}\)

mũ 2

0,(6) mux bằng 0,(6)^x