cho 1/x-1/y-1/z=0 chứng minh xy-yz-xz=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để phân số $\frac{a}{b}$ có nghĩa thì $b\neq 0$
a.
ĐKXĐ: \(\left\{\begin{matrix} 3x-3\neq 0\\ 4-4x\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3(x-1)\neq 0\\ -4(x-1)\neq 0\end{matrix}\right.\Leftrightarrow x-1\neq 0\Leftrightarrow x\neq 1\)
b.
ĐKXĐ: \(\left\{\begin{matrix} a+3\neq 0\\ 3a^2+14a+15\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a+3\neq 0\\ (3a+5)(a+3)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 3a+5\neq 0\\ a+3\neq 0\end{matrix}\right.\Leftrightarrow a\neq \frac{-5}{3}; a\neq -3\)
c.
ĐKXĐ: \(\left\{\begin{matrix} b^3+1\neq 0\\ b^2-b+1\neq 0\\ b+1\neq 0\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b^3+1\neq 0\\ (b+1)(b^2-b+1)\neq 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} b^3+1\neq 0\\ b^3+1\neq 0\end{matrix}\right.\Leftrightarrow b^3\neq -1\Leftrightarrow b\neq -1\)
e.
ĐKXĐ: \(\left\{\begin{matrix} 4x^2-2xy\neq 0\\ 2y^2-4xy\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x(2x-y)\neq 0\\ 2y(y-2x)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ 2x-y\neq 0\\ y-2x\neq 0\\ y\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 0\\ x\neq \frac{y}{2}\\ y\neq 0\\ \end{matrix}\right.\)
h.
ĐKXĐ: \(\left\{\begin{matrix} x-5\neq 0\\ x+5\neq 0\\ 25-x^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-5\neq 0\\\ x+5\neq 0\\ -(x-5)(x+5)\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-5\neq 0\\ x+5\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 5\\ x\neq -5\end{matrix}\right.\)



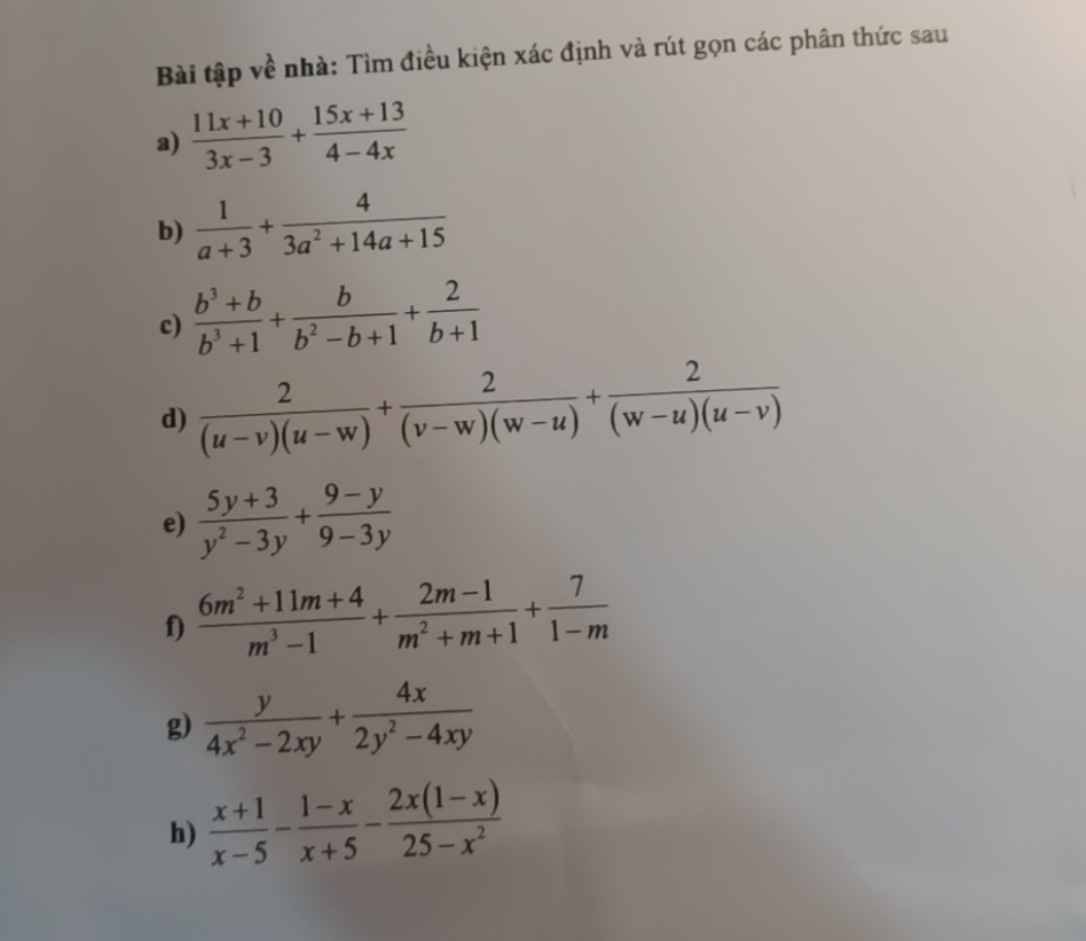
Lời giải:
$\frac{1}{x}-\frac{1}{y}-\frac{1}{z}=0$
$\Leftrightarrow \frac{yz}{xyz}-\frac{xz}{xyz}-\frac{xy}{xyz}=0$
$\Leftrightarrow \frac{yz-xz-xy}{xyz}=0$
$\Leftrightarrow yz-xz-xy=0$
Đây mới đúng nhé bạn. Đoạn biểu thức sau "chứng minh" của bạn có lẽ bị viết sai rồi.