Do I là giao điểm của hai đường phân giác BI và CI của ∆ABC

⇒ AI là đường phân giác của ∆ABC

⇒ ∠MAI = ∠NAI

Xét hai tam giác vuông: ∆AMI và ∆ANI có:

AI là cạnh chung

∠MAI = ∠NAI (cmt)

⇒ AMI = ANI (cạnh huyền - góc nhọn)

⇒ IM = IN (hai cạnh tương ứng)

Hình b tự vẽ nhé
Kẻ IK vuông góc BC
Xét △BMI và △BKI, ta có
Góc BMI= góc BKI = 90^o
Góc MBI= góc IBK ( BI là phân giác góc ABC)
BI cạnh chung
=> △BMI= △BKI (ch-gn)
=> IM= IK ( 2 cạnh tương ứng)
CMTT=> △CNI= △CKI 
=> IN=IK
=> IM=IN

Các bạn trả lời giúp mk. Mk cần gấp lắm

ko bt

Lời giải:

$a^{100}+b^{100}=a^{101}+b^{101}=a^{102}+b^{102}$

$\Rightarrow (a^{101}+b^{101})^2=(a^{100}+b^{100})(a^{102}+b^{102})$

$\Rightarrow a^{202}+b^{202}+2a^{101}.b^{101}=a^{202}+b^{202}+a^{100}b^{102}+a^{102}b^{100}$

$\Rightarrow 2a^{101}b^{101}=a^{100}b^{102}+a^{102}b^{100}$

$\Rightarrow a^{100}b^{100}(a^2+b^2-2ab)=0$

$\Rightarrow a^{100}b^{100}(a-b)^2=0$

$\Rightarrow a=0$ hoặc $b=0$ hoặc $a=b$

Nếu $a=0$ thì:

$b^{100}=b^{101}=b^{102}$

$\Rightarrow b^{100}(b-1)=0$

$\Rightarrow b=0$ hoặc b=1$ (đều tm) 

$\Rightarrow a^{2022}+b^{2023}=0$ hoặc $1$

Nếu $b=0$ thì tương tự, $a=0$ hoặc $a=1$

$\Rightarrow a^{2022}+b^{2023}=0$ hoặc $1$

Nếu $a=b$ thì thay $a=b$ vào điều kiện đề thì:

$2b^{100}=2b^{101}=2b^{102}$

$\Rightarrow b^{100}=b^{101}=b^{102}$

$\Rightarrow b^{100}(b-1)=0$

$\Rightarrow b=0$ hoặc $b=1$ (đều tm) 

Nếu $a=b=0\Rightarrow a^{2022}+b^{2023}=0$

Nếu $a=b=1\Rightarrow a^{2022}+b^{2023}=2$

Vậy $a^{2022}+b^{2023}$ có thể nhận giá trị $0,1,2$

=2 nha

Câu hỏi
# Cho dãy tỉ số bằng nhau ( 2bz-3cy )/a=(3cx az)/2b=(ay-2bx)/3c. Chứng minh: x/a=y/2b=z/3c.
Trả lời
Đáp án:+Giải thích các bước giải:


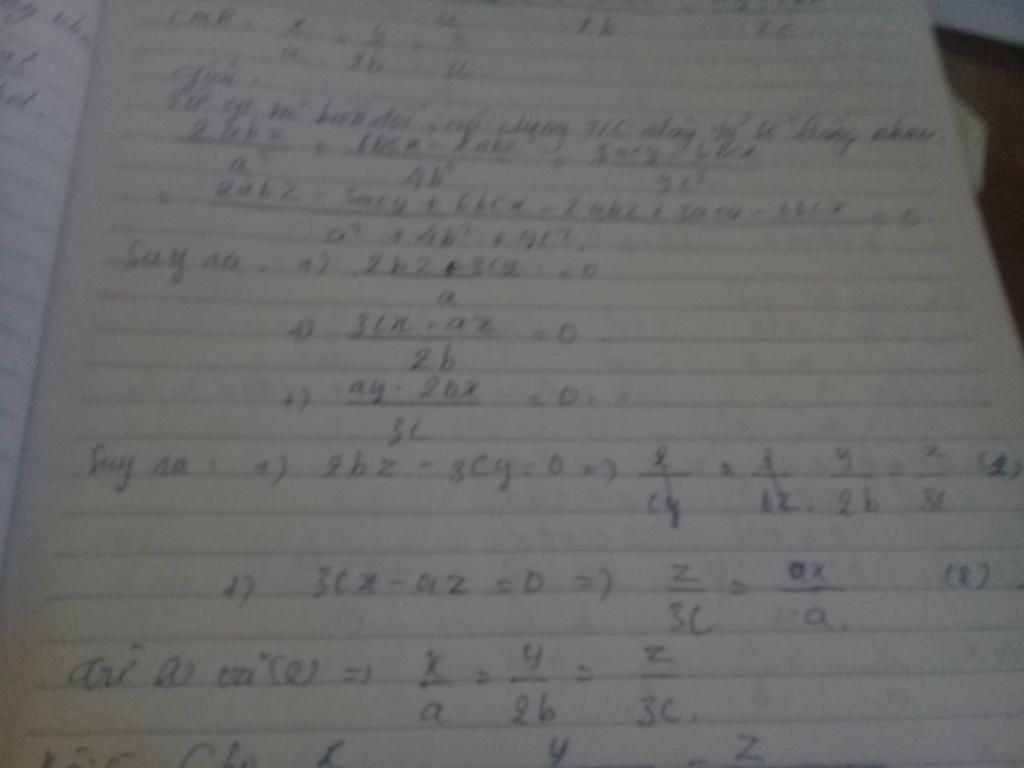
bạn tìm trên link này nhá mk ko gửi hình ảnh đc

Gọi a, b lần lượt là số cây lớp 7A, số cây lớp 7B trồng được

Ta có: \(\dfrac{a}{b}=\dfrac{5}{4}\Rightarrow\dfrac{a}{5}=\dfrac{b}{4}\)

Vì lớp 7A trồng được nhiều hơn lớp 7B 20 cây nên ta có: \(a-b=20\)

Theo tc dãy tỉ số bằng nhau:

\(\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{a-b}{5-4}=20\\ \Rightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{20}{1}=20\\\Rightarrow a=20.5=100;b=20.4=80\)

Như vậy lớp 7A trồng được 100 cây, lớp 7B trồng được 80 cây

Gọi x (cây), y (cây) lần lượt là số cây trồng được của lớp 7A và lớp 7B (x, y ∈ ℕ*)

Do tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 5/4 nên:

x/y = 5/4

⇒ x/5 = y/4

Do số cây của lớp 7A trồng nhiều hơn lớp 7B là 20 cây nên:

x - y = 20

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/5 = y/4 = (x - y)/(5 - 4) = 20/1 = 20

x/5 = 20 ⇒ x = 20.5 = 100

y/4 = 20 ⇒ y = 20.4 = 80

Vậy số cây trồng được của lớp 7A và lớp 7B lần lượt là: 100 cây, 80 cây

a) Ta có:

k = 6/(-3) = -2

⇒ x = -2y

b) x = -2 ⇒ y = -2 : (-2) = 1

x = -1/2 ⇒ y = (-1/2) : (-2) = 1/4

y = -1 ⇒ x = -2.(-1) = 2

x = 0 ⇒ y = 0

y = 8 ⇒ x = -2.8 = -16

y = -6 ⇒ x = -2.(-6) = 12

skillful

?

x gần bằng

5,86388922

File: undefined 

File: undefined 

gay