Hình tứ giác HMIK có góc H = 3x, góc M = 4x, góc I = 2x, góc K = x. Tính số đo các góc. Có phải là hình thang k?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


khai triển đa thức ta đc:
=x2-4x+4+x2+4x+4+x3+9x2+27x+27+27x3+27x2+9x+1
=28x3+36x2+36x+36
Vậy hệ số của x2 sau khi khai triển là 36

Bài 1;
a: ABCD là hình thang cân
=>\(\widehat{D}=\widehat{C}=60^0\)
ABCD là hình thang
=>\(\widehat{BAD}+\widehat{ADC}=180^0\)
=>\(\widehat{BAD}=120^0\)
ABCD là hình thang cân
=>\(\widehat{BAD}=\widehat{ABC}\)
=>\(\widehat{ABC}=120^0\)
b: Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
\(\widehat{ADE}=\widehat{BCF}\)
Do đó: ΔAED=ΔBFC
=>AE=BF
Bài 4:
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>BH=CK
Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
Do đó: ΔKBC=ΔHCB
c: ΔAHB=ΔAKC
=>AH=AK
Xét ΔABC có \(\dfrac{AH}{AC}=\dfrac{AK}{AB}\)
nên KH//BC
Xét tứ giác BKHC có KH//BC và BH=KC
nên BKHC là hình thang cân


a: Ta có: \(\widehat{ICA}+\widehat{ICB}=\widehat{ACB}=90^0\)
\(\widehat{ICB}+\widehat{NCB}=\widehat{NCI}=90^0\)
Do đó: \(\widehat{ICA}=\widehat{NCB}\)
Ta có: \(\widehat{CAI}+\widehat{CBI}=90^0\)(ΔCBA vuông tại C)
\(\widehat{CBI}+\widehat{CBN}=\widehat{NBI}=90^0\)
Do đó: \(\widehat{CAI}=\widehat{CBN}\)
Xét ΔCAI và ΔCBN có
\(\widehat{CAI}=\widehat{CBN}\)
\(\widehat{ICA}=\widehat{NCB}\)
Do đó: ΔCAI~ΔCBN
b: Ta có: \(\widehat{ACM}+\widehat{ACI}=\widehat{ICM}=90^0\)
\(\widehat{ICA}+\widehat{ICB}=\widehat{ACB}=90^0\)
Do đó: \(\widehat{ACM}=\widehat{ICB}\)
Ta có: \(\widehat{CAM}+\widehat{CAB}=\widehat{BAM}=90^0\)
\(\widehat{CAB}+\widehat{CBA}=90^0\)(ΔCAB vuông tại C)
Do đó: \(\widehat{CAM}=\widehat{CBA}\)
Xét ΔCAM và ΔCBI có
\(\widehat{CAM}=\widehat{CBI}\)
\(\widehat{ACM}=\widehat{BCI}\)
Do đó: ΔCAM~ΔCBI
=>\(\dfrac{AC}{CB}=\dfrac{AM}{BI}\)
=>\(AC\cdot BI=MA\cdot BC\)
c: Xét tứ giác CIBN có \(\widehat{ICN}+\widehat{IBN}=90^0+90^0=180^0\)
nên CIBN là tứ giác nội tiếp
=>\(\widehat{CIN}=\widehat{CBN}\)
=>\(\widehat{CIN}=\widehat{BAC}\)

a: \(\left(x+2\right)^2-\left(x-2\right)\left(x+1\right)=3\)
=>\(x^2+4x+4-\left(x^2-x-2\right)=3\)
=>\(x^2+4x+4-x^2+x+2-3=0\)
=>5x+3=0
=>5x=-3
=>\(x=-\dfrac{3}{5}\)
b: \(\left(2x+3\right)^2-4\left(x-1\right)^2=0\)
=>\(\left(2x+3\right)^2-\left(2x-2\right)^2=0\)
=>\(\left(2x+3+2x-2\right)\left(2x+3-2x+2\right)=0\)
=>\(5\left(4x+1\right)=0\)
=>4x+1=0
=>4x=-1
=>\(x=-\dfrac{1}{4}\)
c: \(\left(x+1\right)\left(x^2-x+1\right)-x\left(x^2+2\right)-2=0\)
=>\(x^3+1-x^3-2x-2=0\)
=>-2x-1=0
=>-2x=1
=>\(x=\dfrac{1}{-2}=-\dfrac{1}{2}\)

13: \(x^3-6x^2+12x-8\)
\(=x^3-3\cdot x^2\cdot2+3\cdot x\cdot2^2-2^3\)
\(=\left(x-2\right)^3\)
14: \(8x^3+12x^2y+6xy^2+y^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2+y^3\)
\(=\left(2x+y\right)^3\)
16: \(x^{10}-1=\left(x^5-1\right)\left(x^5+1\right)=\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\left(x+1\right)\left(x^4-x^3+x^2-x+1\right)\)
17: \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
18: \(4x^2-25=\left(2x\right)^2-5^2=\left(2x-5\right)\left(2x+5\right)\)
19: \(x^4-y^4=\left(x^2-y^2\right)\left(x^2+y^2\right)=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\)
20: \(9x^2+6xy+y^2=\left(3x\right)^2+2\cdot3x\cdot y+y^2=\left(3x+y\right)^2\)
21: \(6x-9-x^2=-\left(x^2-6x+9\right)\)
\(=-\left(x^2-2\cdot x\cdot3+3^2\right)\)
\(=-\left(x-3\right)^2\)
22: \(x^2+4xy+4y^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=\left(x+2y\right)^2\)
23: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)\left(x+y+x-y\right)\)
\(=2x\cdot2y=4xy\)
24: \(\left(x+y+z\right)^2-4z^2\)
\(=\left(x+y+z\right)^2-\left(2z\right)^2\)
\(=\left(x+y+z-2z\right)\left(x+y+z+2z\right)\)
\(=\left(x+y-z\right)\left(x+y+3z\right)\)
25: \(\left(3x+1\right)^2-\left(x+1\right)^2\)
\(=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\)
\(=2x\left(4x+2\right)=4x\left(2x+1\right)\)
26: \(x^3y^3+125=\left(xy\right)^3+5^3\)
\(=\left(xy+5\right)\left(x^2y^2-5xy+25\right)\)
27: \(8x^3-y^3-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2\right)-6xy\left(2x-y\right)\)
\(=\left(2x-y\right)\left(4x^2+2xy+y^2-6xy\right)\)
\(=\left(2x-y\right)\left(4x^2-4xy+y^2\right)=\left(2x-y\right)^3\)
28: \(\left(3x+2\right)^2-2\left(x-1\right)\left(3x+2\right)+\left(x-1\right)^2\)
\(=\left(3x+2-x+1\right)^2\)
\(=\left(2x+3\right)^2\)

a: Xét ΔABC có D,E lần lượt là trung điểm của AC,AB
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{BC}{2}=2\left(cm\right)\)
Xét hình thang BEDC có
M,N lần lượt là trung điểm của EB,DC
=>MN là đường trung bình của hình thang BEDC
=>MN//ED//BC và \(MN=\dfrac{ED+BC}{2}=\dfrac{2+4}{2}=3\left(cm\right)\)
b: Xét ΔBED có MP//ED
nên \(\dfrac{MP}{ED}=\dfrac{BM}{BE}=\dfrac{1}{2}\)
=>\(MP=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)
Xét ΔCED có NQ//ED
nên \(\dfrac{NQ}{ED}=\dfrac{CN}{CD}=\dfrac{1}{2}\)
=>\(NQ=\dfrac{1}{2}ED=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BC=\dfrac{1}{4}BC\)
\(MN=\dfrac{1}{2}\left(ED+BC\right)=\dfrac{1}{2}\left(\dfrac{1}{2}BC+BC\right)=\dfrac{1}{2}\cdot\dfrac{3}{2}BC=\dfrac{3}{4}BC\)
=>\(MP+PQ+QN=\dfrac{3}{4}BC\)
=>\(PQ=\dfrac{3}{4}BC-\dfrac{1}{4}BC-\dfrac{1}{4}BC=\dfrac{1}{4}BC\)
Do đó:MP=PQ=QN

\(a.4x-6y=2\left(2x-3y\right)\\ b.x^2+6x+9-y^2\\ =\left(x+3\right)^2-y^2\\ =\left(x-y+3\right)\left(x+y+3\right)\\ c.4x^2-9y^2\\ =\left(2x\right)^2-\left(3y\right)^2\\ =\left(2x-3y\right)\left(2x+3y\right)\\ d.x^2-x-y^2+y\\ =\left(x^2-y^2\right)-\left(x-y\right)\\ =\left(x+y\right)\left(x-y\right)-\left(x-y\right)\\ =\left(x-y\right)\left(x+y-1\right)\\ e.x^2-4y^2-6x+9\\ =\left(x^2-6x+9\right)-4y^2\\ =\left(x-3\right)^2-\left(2y\right)^2\\ =\left(x-2y-3\right)\left(x+2y-3\right)\\ f.x^4-y^4+4y^2-4\\ =x^4-\left(y^4-4y^2+4\right)\\ =\left(x^2\right)^2-\left(y^2-2\right)^2\\ =\left(x^2-y^2+2\right)\left(x^2+y^2-2\right)\)

Câu 2:
\(A=x^2-10x+1\\ =\left(x^2-10x+25\right)-24\\ =\left(x-5\right)^2-24\ge-24\forall x\)
Dấu "=" xảy ra: `x-5=0<=>x=5`
\(B=x^2-5x+2\\ =\left(x^2-5x+\dfrac{25}{4}\right)-\dfrac{17}{4}\\ =\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right)-\dfrac{17}{4}\\ =\left(x-\dfrac{5}{2}\right)^2-\dfrac{17}{4}\ge-\dfrac{17}{4}\forall x\)
Dấu "=" xảy ra: `x-5/2=0<=>x=5/2`
Câu 2
A = x² - 10x + 1
= x² + 2.x.5 + 25 - 24
= (x + 5)² - 24
Do (x + 5)² ≥ 0 với mọi x ∈ R
⇒ (x + 5)² - 24 ≥ -24 (với mọi x ∈ R)
Vậy GTNN của A là -24 khi x = -5
B = x² - 5x + 2
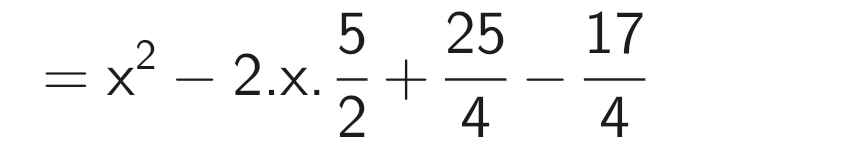
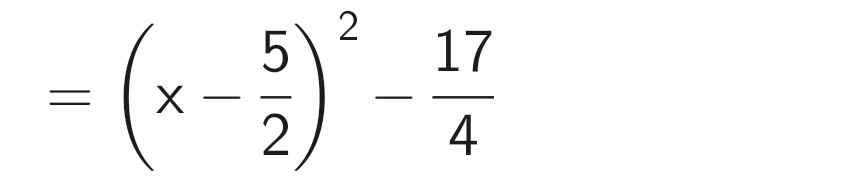
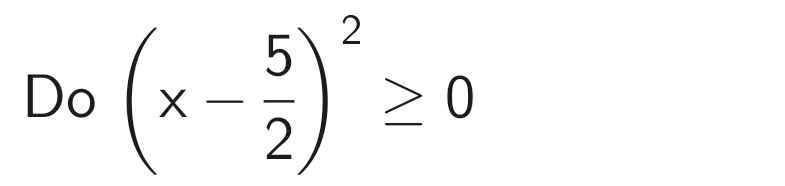
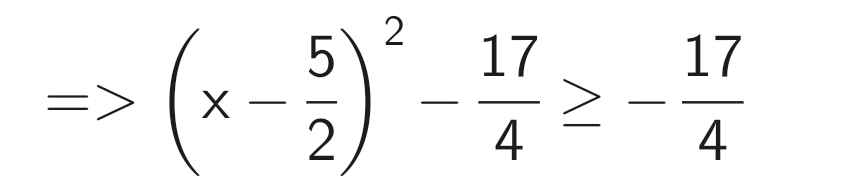
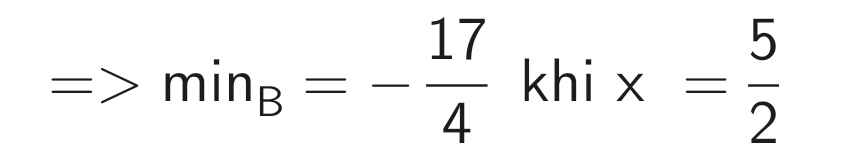


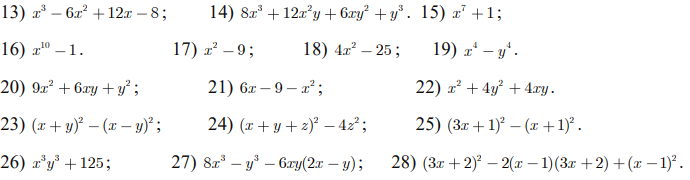
Xét tứ giác HMIK có \(\widehat{H}+\widehat{M}+\widehat{I}+\widehat{K}=360^0\)
=>\(3x+4x+2x+x=360\)
=>\(10x=360^0\)
=>\(x=36^0\)
=>\(\widehat{H}=3\cdot36^0=108^0;\widehat{M}=4\cdot36^0=144^0;\widehat{I}=2\cdot36^0=72^0;\widehat{K}=36^0\)
Vì \(\widehat{H}+\widehat{I}=180^0\)
nên HM//IK
=>HMIK là hình thang