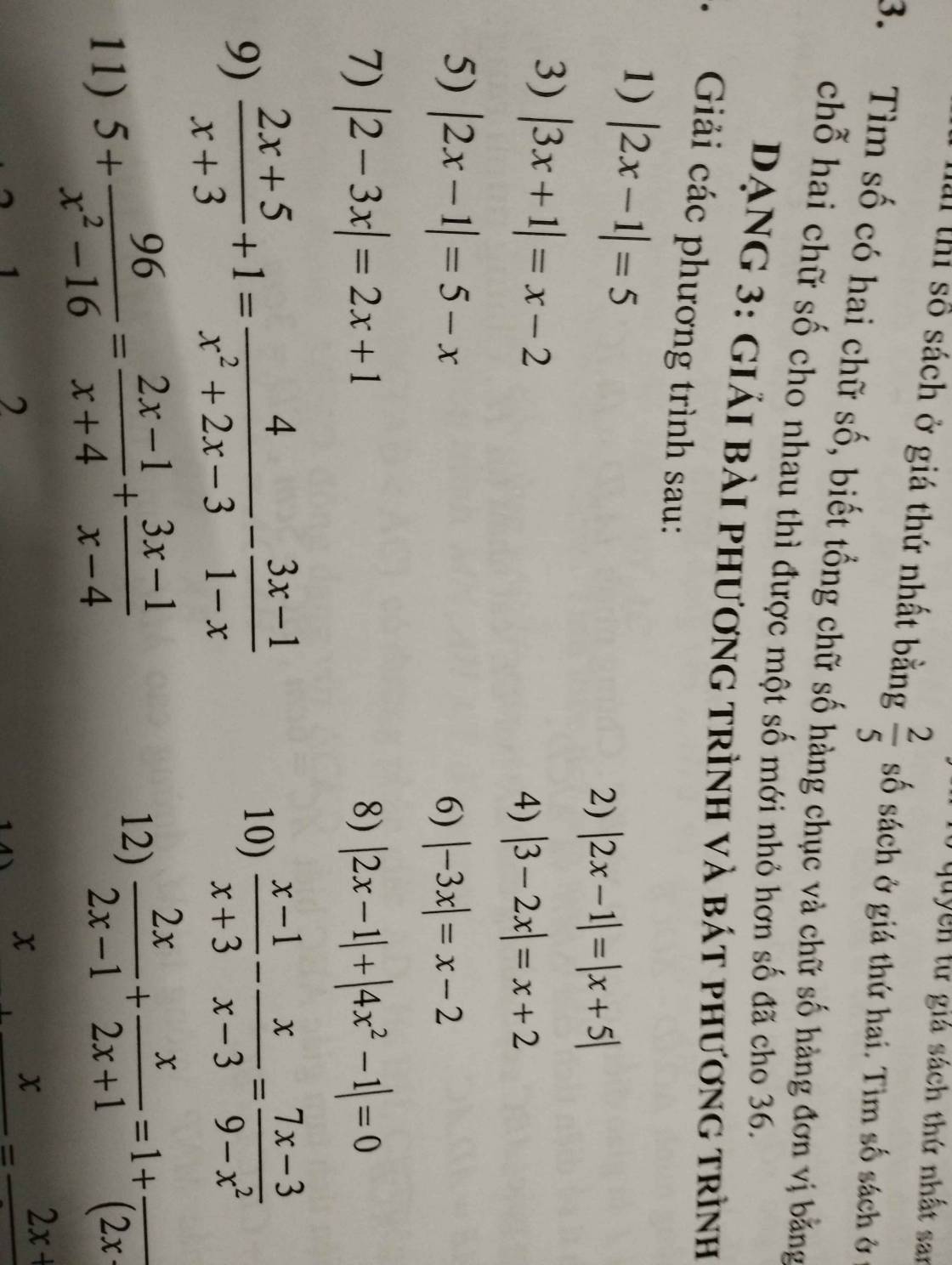cho tam giác ABC vuông tại A ( AB<AC) đường cao AH. Qua B vẽ đường thẳng song song với AC cắt AH tại D. a/ chứng minh tam giác AHC đồng dạng với tam giác DHB. b/ Chứng minh: AB^2=AC*BD.c/ Gọi M, N lần lượt là trung điểm của BD, AC. Chứng minh ba điểm M, H, N thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Có \(\left|2x+1\right|\ge0;\left|4x^2-1\right|\ge0\forall x\)
\(\Rightarrow\left|2x+1\right|+\left|4x^2-1\right|\ge0\forall x\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}2x+1=0\\4x^2-1=0\end{matrix}\right.\Leftrightarrow x=-\dfrac{1}{2}\)
c) \(\left|2x-1\right|=\left|x+5\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+5\\2x-1=-x-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-\dfrac{4}{3}\end{matrix}\right.\)

Lời giải:
$|2x-1|=|x+5|$
$\Rightarrow 2x-1=x+5$ hoặc $2x-1=-(x+5)$
$\Rightarrow x=6$ hoặc $x=\frac{-4}{3}$

Hai xe cùng vận tốc, đi vào thời gian khác nhau thì làm sao đến B cùng 1 lúc hả bạn? Bạn xem lại.

Gọi lượng dầu thùng thứ hai là: \(x\) ( \(x>0\))
Thì lượng dầu thùng thứ nhất là: 2\(x\)
Theo bài ra ta có : 2\(x\) - 10 = \(x\) + 10
2\(x\) - 10 - \(x\) - 10 = 0
\(x\) - 20 = 0
\(x\) = 20
Vậy thùng thứ hai chứa 10 l dầu.
Thùng thứ nhất chứa 20 \(\times\) 2 = 40 (l)
Kết luận: Thùng thứ nhất chứa 40 l đầu
Thùng thứ hai chứa 20 l dầu

Lời giải:
a.
PT $\Leftrightarrow 3x^2+\frac{x}{2}-3x^2+3x+2=0$
$\Leftrightarrow \frac{7}{2}x+2=0$
$\Leftrightarrow \frac{7}{2}x=-2$
$\Leftrightarrow x=-2: \frac{7}{2}=\frac{-4}{7}$
b.
PT $\Leftrightarrow 5x^2-3-5x^2-6x=0$
$\Leftrightarrow -3-6x=0$
$\Leftrightarrow 6x=-3$
$\Leftrightarrow x=\frac{-3}{6}=\frac{-1}{2}$