Do 38,1 < x < 39,1 nên x = 39

a) Quãng đường người đó đi được trong 3 giờ đầu:

35,7 × 3 = 107,1 (km)

Đoạn đường còn lại người đó đi bằng xe máy:

252,1 - 107,1 = 145 (km)

b) Thời gian người đó đi hết quãng đường còn lại:

145 : 29 = 5 (giờ)

Người đó đến B lúc:

5 giờ 15 phút + 15 phút + 3 giờ + 5 giờ = 13 giờ 30 phút

     ^{Olm chào em, đây là dạng toán nâng cao chuyên đề toán hai tỉ số, cấu trúc thi chuyên Amsterdam, thi học sinh giỏi, thi violympic. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết bài này bằng sơ đồ đoạn thẳng của tiểu học như sau:}

                      ^Giải:

^{Sau khi cắt bớt \(\dfrac{3}{8}\) tấm vải xanh thì còn lại là: 1 - \(\dfrac{3}{8}\) = \(\dfrac{5}{8}\) (tấm vải xanh)}

^{Sau khi cắt bớt \(\dfrac{7}{12}\) tấm vải đỏ thì còn lại là:  1 - \(\dfrac{7}{12}\) = \(\dfrac{5}{12}\) (tấm vải đỏ)}

  ^{\(\dfrac{5}{8}\) tấm vải xanh và \(\dfrac{5}{8}\) tấm vải đỏ ứng với số mét là: 108 x \(\dfrac{5}{8}\) = 67,5 (m)}

^{Theo bài ra ta có sơ đồ:} 

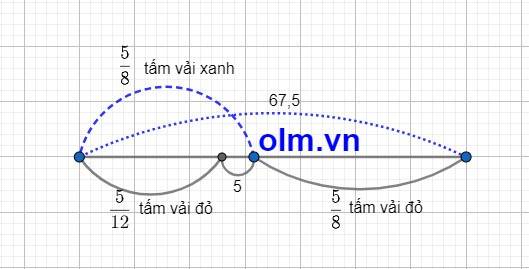
Theo sơ đồ ta có: 

 \(\dfrac{5}{12}\) tấm vải đỏ và \(\dfrac{5}{8}\) tấm vải đỏ ứng với số mét là:

                        67,5 - 5 = 62,5 (m)

\(\dfrac{5}{12}\) tấm vải đỏ và \(\dfrac{5}{8}\) tấm vải đỏ ứng với phân số là: 

                       \(\dfrac{5}{12}\) + \(\dfrac{5}{8}\) = \(\dfrac{25}{24}\) (tấm vải đỏ)

Tấm vải đỏ dài là: 62,5 : \(\dfrac{25}{24}\) = 60 (m)

Tấm vải xanh dài là: 108 - 60 = 48 (m)

Đáp số: Tấm vải xanh dài 48 m

              Tấm vải đỏ dài 60 m

Olm chào em, đây là dạng toán nâng cao toán hai tỉ số trong đó có một đại lượng không đổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm.vn sẽ hướng dẫn các em làm chi tiết dạng này như sau:

       Bước 1: Lập luận chỉ ra đại lượng không đổi

       Bước 2: Thông qua hai tỉ số tìm được đại lượng không đổi

       Bước 3: Qua đại lượng không đổi, tìm được hai số cần tìm.

                                            Giải

    Dù Hoa cho Lan bao nhiêu cái bánh và ngược lại thì tổng số cái bánh của hai bạn vẫn luôn không đổi

      Số bánh của Hoa sau khi cho đi 100 cái bánh bằng:

                    3 : (1 + 3) = \(\dfrac{3}{4}\) (tổng số bánh của Hoa và Lan)

      Số bánh của Hoa sau khi nhận 100 cái bánh bằng:

             5 : (1 + 5) = \(\dfrac{5}{6}\) (tổng số bánh của Hoa và Lan)

    \(\dfrac{5}{6}\) tổng số bánh của Hoa và Lan hơn \(\dfrac{3}{4}\) tổng số bánh của Hoa và Lan là:

             \(\dfrac{5}{6}\) - \(\dfrac{3}{4}\) = \(\dfrac{1}{12}\) (tổng số bánh của Hoa và Lan)

\(\dfrac{1}{12}\) tổng số bánh của Hoa và Lan ứng với số bánh là:

            100 + 100 = 200 (cái bánh)

Tổng số bánh của Hoa và Lan là: 

            200 : \(\dfrac{1}{12}\) = 2400 (cái bánh)

Số bánh của Hoa sau khi cho Lan 100 cái bánh là: 

           2400 x \(\dfrac{3}{4}\) = 1800 (cái bánh)

Số bánh của Hoa là: 1800 + 100 = 1900 (cái bánh)

Đáp số: 1900 cái bánh. 

Môn Toán ở bậc Tiểu học có vai trò rất quan trọng đó là cung cấp những kiến thức cơ sở, nền tảng về Toán học, rèn luyện kỹ năng tính toán, giải toán, suy luận đơn giản, đồng thời góp phần rèn luyện các phẩm chất đạo đức, tính kiên trì sáng tạo ở mỗi con người. Các kiến thức và kĩ năng của môn Toán có nhiều ứng dụng trong đời sống rất cần thiết cho con người lao động mới, tạo tiền đề cho các môn học khác và bậc học cao hơn.

Yếu tố đại số là một trong những nội dung của chương trình môn Toán Tiểu học. Nếu như số học là nội dung trọng tâm cơ bản xuyên suốt quá trình học Toán ở Tiểu học thì các yếu tố đại số trong môn Toán lại góp phần để cung cấp kiến thức và nâng cao kỹ năng số học. Như vậy yếu tố đại số đóng vai trò rất quan trọng: Nó kết hợp chặt chẽ với số học không những nhằm mục đích củng cố, truyền tải nội dung số học mà còn góp phần tạo điều kiện để học sinh phát triển trí thông minh, tư duy độc lập, linh hoạt sáng tạo.

Mặt khác, ở những bậc học tiếp theo không thể thiếu được môn Đại số mà các yếu tố đại số trong môn Toán tại Tiểu học chính là sự chuẩn bị ban đầu cho môn học này. Sự chuẩn bị ban đầu là quan trọng, nhưng sự chuẩn bị có trở nên tốt đẹp và vững chắc hay không phụ thuộc phần lớn vào người giáo viên Tiểu học. Đối với mỗi giáo viên Tiểu học, nhà trường sư phạm đã trang bị cho giáo viên lý thuyết về phương pháp dạy học nhưng lý thuyết chỉ là màu xám mà thực tiễn mới trở nên sinh động. Vì vậy, trước yêu cầu đổi mới phương pháp dạy học như hiện nay, tìm hiểu việc dạy học các yếu tố đại số ở Tiểu học là điều hết sức cần thiết. Qua quá trình tìm hiểu, nghiên cứu cùng những kinh nghiệm rút ra trong dạy học, qua tham khảo đồng nghiệp trong và ngoài đơn vị đã giúp tôi thấy được mối liên hệ giữa cơ sở lí luận và thực tiễn dạy học từ đó tìm ra những giải pháp nâng cao chất lượng dạy học các yếu tố đại số ở Tiểu học bước đầu ứng dụng giảng dạy tại đơn vị có hiệu quả. Bởi vậy, tôi chọn đề tài “Một số giải pháp nâng cao chất lượng dạy học các yếu tố đại số ở Tiểu học”.

Vận tốc của ô tô đi từ B là:

\(60:\dfrac{3}{2}=60:1,5=40\left(\dfrac{km}{h}\right)\)

Tổng vận tốc hai xe là:

60+40=100(km/h)

Hai xe gặp nhau sau khi đi được:

200:100=2(giờ)

a: Tổng vận tốc hai xe là:

36+16=52(km/h)

Hai người gặp nhau sau:

65:52=1,25(giờ)

b: Chỗ gặp nhau cách A:

1,25x36=45(km)

10h30p-9h=1h30p=1,5(giờ)

Tổng vận tốc hai xe là:

120:1,5=80(km/h)

Tổng số phần bằng nhau là:

2+3=5(phần)

Vận tốc của xe máy là 80:5x2=32(km/h)

Vận tốc của ô tô là 80-32=48(km/h)

Thời gian từ nhà tới trường của Nam là:

7 giờ 30 phút - 6 giờ 50 phút = 40 phút

40'

\(\dfrac{5}{9\times11}+\dfrac{5}{11\times13}+...+\dfrac{5}{143\times145}\)

\(=\dfrac{5}{2}\left(\dfrac{2}{9\times11}+\dfrac{2}{11\times13}+...+\dfrac{2}{143\times145}\right)\)

\(=\dfrac{5}{2}\left(\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}+...+\dfrac{1}{143}-\dfrac{1}{145}\right)\)

\(=\dfrac{5}{2}\times\left(\dfrac{1}{9}-\dfrac{1}{145}\right)=\dfrac{5}{2}\times\dfrac{136}{1305}=\dfrac{68}{261}\)