Lời giải:

Giả sử sau $x$ giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách từ xe máy đến M

Có: $AM=MB = AB:2=540:2=270$ (km) 

Sau $x$ giờ thì ô tô còn cách $M$: $270-65x$ (km)

Sau $x$ giờ thì xe máy còn cách $M$: $270-40x$ (km) 

Có:

$270-65x=\frac{1}{2}(270-40x)$

$\Rightarrow x=3$ (giờ)

2+3=5=2^1+3^1=5^1

Vậy x=1

GIÚP MIK VỚI, MIK ĐANG CẦN GẤP!!!!!

Yêu cầu và điều kiện đề bài là gì bạn cần ghi chú rõ nhé.

53+532+...+5320=5(13+132+...+1320)53+532+...+5320=5(13+132+...+1320)

Gọi A=13+132+...+1320�=13+132+...+1320. Ta có

3A=1+13+...+13193�=1+13+...+1319

3A−A=(1+13+...+1319)−(13+132+...+1320)3�−�=(1+13+...+1319)−(13+132+...+1320)

2A=1−13202�=1−1320

A=1−13202�=1−13202

Suy ra 53+532+...+5320=5(13+132+...+1320)=5⋅1−13202=5−53202

Lời giải:

Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:

$|x-2021|+|x-2023|=|x-2021|+|2023-x|\geq |x-2021+2023-x|=2$

$|x-2022|\geq 0$ (tính chất trị tuyệt đối)

$\Rightarrow A=|x-2021|+|x-2022|+|x-2023|\geq 2+0=2$

Vậy $A_{\min}=2$. Giá trị này đạt tại $(x-2021)(2023-x)\geq 0$ và $x-2022=0$

Hay $x=2022$

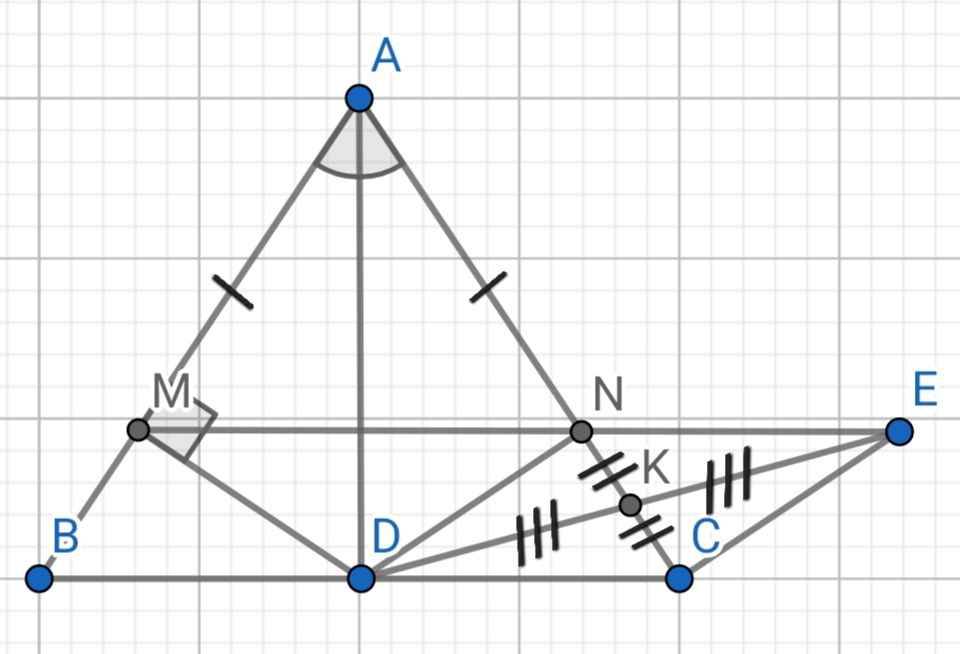 a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

⇒ BD = CD

⇒ D là trung điểm của BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

b) Sửa đề: Chứng minh ∆ADM = ∆ADN

Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)

⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)

⇒ DN ⊥ AN

⇒ DN ⊥ AC

d) Do K là trung điểm của CN (gt)

⇒ CK = KN

Xét ∆DKC và ∆EKN có:

CK = KN (cmt)

∠DKC = ∠EKN (đối đỉnh)

KD = KE (gt)

⇒ ∆DKC = ∆EKN (c-g-c)

⇒ ∠KDC = ∠KEN (hai góc tương ứng)

Mà ∠KDC và ∠KEN là hai góc so le trong

⇒ EN // CD

⇒ EN // BC (3)

∆AMN có:

AM = AN (gt)

⇒ ∆AMN cân tại A

⇒ ∠AMN = (180⁰ - ∠MAN) : 2

= (180⁰ - ∠BAC) : 2 (4)

∆ABC cân tại A (gt)

⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)

Từ (4) và (5) ⇒ ∠AMN = ∠ABC

Mà ∠AMN và ∠ABC là hai góc đồng vị

⇒ MN // BC (6)

Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

\(\left|2\dfrac{1}{5}-x\right|\)\(+\left|x-\dfrac{1}{5}\right|\)\(+8\dfrac{1}{5}\)\(=1,2\)

\(\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=\dfrac{6}{5}-\dfrac{41}{5}\)

\(\Rightarrow\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|=\dfrac{-36}{5}\) (vô lý vì \(\left|2\dfrac{1}{5}-x\right|+\left|x-\dfrac{1}{5}\right|\ge0\))

Vậy: Không tìm được giá trị x thoả mãn.

Lời giải:

Áp dụng TCDTSBN:

\(\frac{x-1}{2005}=\frac{3-y}{2000}=\frac{x-1+3-y}{2005+2000}=\frac{x-y+2}{4005}=\frac{4009+2}{4005}=\frac{4011}{4005}\)

\(\Rightarrow x-1=\frac{4011}{4005}.2005\Rightarrow x=\frac{536404}{267}\\ 3-y=\frac{4011}{4005}.2000\Rightarrow y\approx -2000\)