
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3^{400}=\left(3^4\right)^{100}=81^{100};5^{300}=\left(5^3\right)^{100}=125^{100}\)
mà 81<125
nên \(3^{400}< 5^{300}\)

Số tự nhiên chia 2 dư 1 có dạng tổng quát là \(2k+1\)

Bài 2:
a: Xét ΔABC vuông tại A có
\(sin\alpha=sinB=\dfrac{AC}{BC}\)
\(cos\alpha=cosB=\dfrac{AB}{BC}\)
\(tan\alpha=tanB=\dfrac{AC}{AB}\)
\(cot\alpha=cotB=\dfrac{AB}{AC}\)
b: \(sin^2\alpha+cos^2\alpha=\left(\dfrac{AB}{BC}\right)^2+\left(\dfrac{AC}{BC}\right)^2\)
\(=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
\(tan\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{sin\alpha}{cos\alpha}\)
\(cot\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{cos\alpha}{sin\alpha}\)
c:
A: \(sin^2\alpha+cos^2\alpha=sin^2\left(\dfrac{1}{3}\right)+cos^2\left(\dfrac{1}{3}\right)=1\)
B: \(\dfrac{sin35^0}{cos35^0}\cdot tan55^0+\dfrac{cos55^0}{sin55^0}\cdot cot55^0\)
\(=\dfrac{cos55}{sin55}\cdot\dfrac{sin55^0}{cos55^0}+\dfrac{cos55^0}{sin55^0}\cdot tan55^0\)
=1+1
=2
C: \(cos^242^0+cos^253^0+cos^248^0+cos^237^0+cos^245^0\)
\(=\left(sin^242^0+cos^242^0\right)+\left(sin^237^0+cos^237^0\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot\dfrac{\left(1-x\right)^2}{2}\)
\(=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(\sqrt[]{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\cdot\dfrac{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}-2}{1}\cdot\dfrac{\sqrt{x}-1}{2}=-\sqrt{x}\left(\sqrt{x}-1\right)\)
b: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)
\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-2x}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}-1-2\sqrt{x}+6}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt[]{x}-3\right)}{-\sqrt{x}+5}\)
\(=\dfrac{x+3\sqrt{x}}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-5}=\dfrac{x}{\sqrt{x}-5}\)
c: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(\overline{cab}=3\cdot\overline{ab}+8\)
=>\(100c+10a+b-30a-3b-8=0\)
=>-20a-2b+100c-8=0
=>\(\left(a;b;c\right)\in\left\{\left(4;6;1\right);\left(9;6;2\right)\right\}\)
Vậy: Số cần tìm là 461;962

Gọi tuổi mẹ là x(tuổi)
(Điều kiện: x>0)
Tuổi con là \(\dfrac{3}{5}x\left(tuổi\right)\)
Tuổi mẹ cách đây 9 năm là x-9(tuổi)
Tuổi con cách đây 9 năm là \(\dfrac{3}{5}x-9\left(tuổi\right)\)
Tuổi mẹ gấp đôi tuổi con nên \(x-9=2\left(\dfrac{3}{5}x-9\right)\)
=>\(\dfrac{6}{5}x-18=x-9\)
=>\(\dfrac{1}{5}x=9\)
=>x=45(nhận)
vậy: Tuổi mẹ là 45 tuổi
Tuổi con là \(\dfrac{3}{5}\cdot45=27\left(tuổi\right)\)

a: Gọi số ban đầu có dạng là \(\overline{ab7}\)
Số mới được tạo ra khi chuyển chữ số 7 lên đầu là \(\overline{7ab}\)
Chia số mới cho số cũ thì được thương là 2,dư là 21
nên ta có: \(\overline{7ab}=2\cdot\overline{ab7}+21\)
=>\(700+\overline{ab}=2\left(10\overline{ab}+7\right)+21\)
=>\(\overline{ab}-20\overline{ab}=14+21-700\)
=>\(-19\overline{ab}=-665\)
=>\(\overline{ab}=35\)
vậy: Số ban đầu là 357
b: Trong 3 số tự nhiên liên tiếp, chắc chắn sẽ có số chia hết cho 3
=>Tích của 3 số tự nhiên liên tiếp sẽ luôn chia hết cho 3

ĐKXĐ: \(x\ne2\)
\(P=\dfrac{x^4-16}{x^4-4x^3+8x^2-16x+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^4+4x^2-4x^3-16x+4x^2+16}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x^2+4\right)}{x^2\left(x^2+4\right)-4x\left(x^2+4\right)+4\left(x^2+4\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x^2-4x+4}=\dfrac{x+2}{x-2}\)
Để P nguyên thì \(x+2⋮x-2\)
=>\(x-2+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)

Sửa đề: \(\dfrac{2020^3-1}{2020^2+2021}\)
\(=\dfrac{\left(2020-1\right)\left(2020^2+2020+1\right)}{2020^2+2020+1}\)
=2020-1=2019
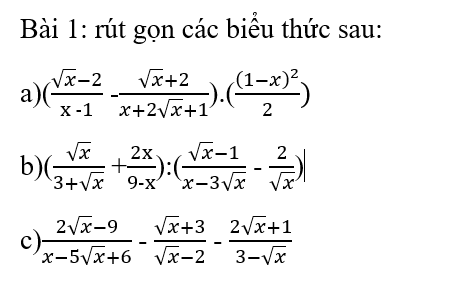
Số bưu ảnh của Hoa là:
(134+14-16):3=132:3=44(cái)
Số bưu ảnh của hồng là 44-14=30(cái)
Số bưu ảnh của Huệ là 44+16=60(cái)