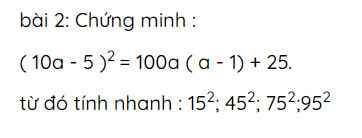Cho hình bình hành ABCD, trên các cạnh AB, BC, CD, DA theo thứ tự lấy các điển M,N,P,Q sao cho AM=CP,BN=DQ.
a) CM:AMCP là hbh
b)Gọi O là giao điểm 2 đg chéo AC và BD, CM o là trung điểm MP
c)CM:MNPQ là hbh
d)CM: AC,BD,MP,NQ đồng quy tại 1 điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`#040911`
`2,`
`(10a - 5)^2 = 100a (a - 1) + 25`
`\Leftrightarrow (10a)^2 - 2. 10a. 5 + 5^2 = 100a^2 - 100a + 25`
`\Leftrightarrow 100a^2 - 100a + 25 = 100a^2 - 100a + 25 (\text {luôn đúng})`
Vậy, `(10a - 5)^2 = 100a (a - 1) + 25`
____
`15^2 = 100. 2( 2 - 1) + 25 = 200 . 1 + 25 = 200 + 25 = 225`
`45^2 = 100. 5(5 - 1) + 25 = 500. 4 + 25 = 2000 + 25 = 2025`
`75^2 = 100. 8(8 - 1) + 25 = 800 . 7 + 25 = 5600 + 25 = 5625`
`95^2 = 100. 10(10 - 1) + 25 = 1000. 9 + 25 = 9000 + 25 = 9025`
_____
Tính nhẩm bình phương của 1 số có chữ số tận cùng là 5
1. Tìm stn a để số đã cho viết được dưới dạng 10a - 5
2. Lấy giá trị a đã tìm được vào biểu thức.

1, \(x^2\) - \(x\) + \(\dfrac{1}{4}\) = 0
\(x^2\) - 2.\(x\).\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) = 0
(\(x\) - \(\dfrac{1}{2}\))2 = 0
\(x\) - \(\dfrac{1}{2}\) =0
\(x\) = \(\dfrac{1}{2}\)
2, \(x^2\) - 10\(x\) = -25
\(x^2\) - 10\(x\) + 25 = 0
(\(x\) - 5)2 = 0
\(x\) - 5 =0
\(x\) = 5

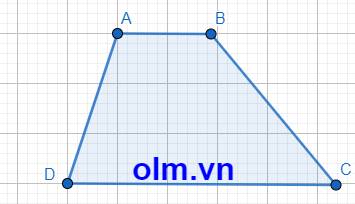
Vì AB//CD nên Góc A và góc D là hai góc trong cùng phía
\(\widehat{A}\)+ \(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) + 3\(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) = 1800:4 = 450
\(\widehat{A}\) = 450.3 =1350
\(\widehat{B}\)+\(\widehat{C}\) = 1800 ⇒ \(\widehat{B}\) + \(\widehat{B}\) - 300 = 1800 ⇒2\(\widehat{B}\) =2100 ⇒ \(\widehat{B}\) = 1050
\(\widehat{C}\) = 1050 - 300 = 750


Diện tích hình bình hành ABCD
\(S_{ABCD}=AC.AD=4.3=12\left(cm^2\right)\)

(2\(x\) + 1)3
= (2\(x\))3 + 3.(2\(x\))2 + 3.2\(x\).12 + 13
= 8\(x^3\) + 12\(x^2\) + 6\(x\) + 1