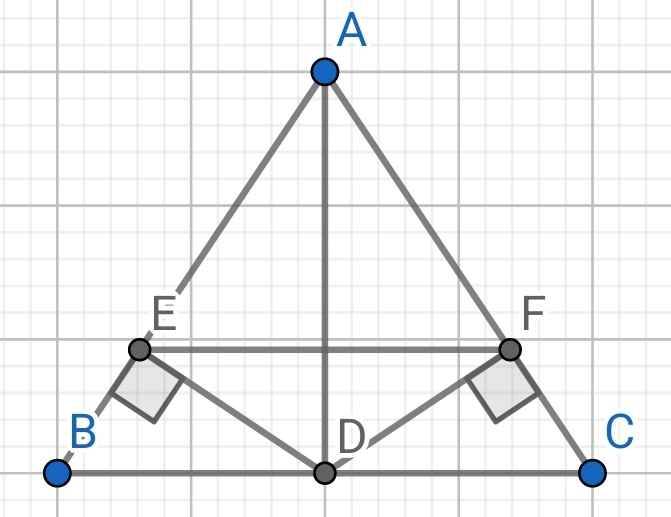
a: Sửa đề: ΔAHD=ΔAED

Xét ΔAHD vuông tại H và ΔAED vuông tại E có

AD chung

AH=AE

Do đó: ΔAHD=ΔAED

=>\(\widehat{HAD}=\widehat{EAD}\)

=>\(\widehat{HAD}=\widehat{CAD}\)

=>AD là phân giác của góc HAC

b: Ta có: ΔAHD=ΔAED

=>DH=DE

Xét ΔDHK vuông tại H và ΔDEC vuông tại E có

DH=DE

\(\widehat{HDK}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDHK=ΔDEC
=>DK=DC

=>ΔDKC cân tại D

c: Ta có: ΔDHK=ΔDEC

=>HK=EC

Xét ΔAKC có \(\dfrac{AH}{HK}=\dfrac{AE}{EC}\)

nên HE//KC

d: Ta có: AH+HK=AK

AE+EC=AC

mà AH=AE và HK=EC

nên AK=AC

=>A nằm trên đường trung trực của KC(1)

ta có: DK=DC

=>D nằm trên đường trung trực của KC(2)

Ta có: IK=IC

=>I nằm trên đường trung trực của CK(3)

Từ (1),(2),(3) suy ra A,D,I thẳng hàng

Lời giải:
Tỉ số vận tốc xe con so với xe khách: $\frac{3}{2}$

Vận tốc xe con là: $20:(3-2)\times 3=60$ (km/h) 

Vận tốc xe khách là: $20:(3-2)\times 2=40$ (km/h) 

Vận tốc xe tải là: $60\times 2:4=30$ (km/h) 

b.

Quãng đường AB dài: $30\times 4=120$ (km)

 Thay \(x=3\) vào đk đề cho, ta có:

\(4f\left(3\right)=0\Leftrightarrow f\left(3\right)=0\) \(\Rightarrow\) \(x=3\) là một nghiệm của \(f\left(x\right)\)

 Thay \(x=-1\) vào đk đề cho, ta có:

\(-4f\left(-3\right)=0\) \(\Leftrightarrow f\left(-3\right)=0\) \(\Rightarrow x=-3\)  là một nghiệm khác của \(f\left(x\right)\)

 \(\Rightarrow f\left(x\right)\) có ít nhất 2 nghiệm (đpcm)

a: x,y là hai đại lượng tỉ lệ nghịch

=>\(x_1\cdot y_1=x_2\cdot y_2\)

=>\(\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}\)

=>\(\dfrac{y_1}{2}=\dfrac{y_2}{3}\)

mà \(2y_1+3y_2=-26\)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{y_1}{2}=\dfrac{y_2}{3}=\dfrac{2y_1+3y_2}{2\cdot2+3\cdot3}=\dfrac{-26}{13}=-2\)

=>\(y_1=-2\cdot2=-4;y_2=-2\cdot3=-6\)

b: \(x_1\cdot y_1=x_2\cdot y_2\)

=>\(-10\cdot x_1=-4\cdot y_2\)

=>\(5x_1=2y_2\)

=>\(\dfrac{x_1}{2}=\dfrac{y_2}{5}\)

mà \(3x_1-2y_2=-32\)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x_1}{2}=\dfrac{y_2}{5}=\dfrac{3x_1-2y_2}{3\cdot2-2\cdot5}=\dfrac{-32}{6-10}=\dfrac{-32}{-4}=8\)

=>\(x_1=8\cdot2=16;y_2=5\cdot8=40\)

 Biến cố có xác suất cao nhất mình có thể nghĩ ra là biến cố: "Lấy ra được một quả bóng không phải là bóng màu xanh." Xác suất đó lên tới \(\dfrac{4}{5}\).

 Hoặc có thể là "Bóng được chọn không có màu đen." đây là biến cố chắc chắn (xác suất 100%). Bạn cần phải bổ sung thêm cho điều kiện đề bài nhé.

a: Xét ΔABD vuông tại A và ΔAHD vuông tại H có

AD chung

\(\widehat{BAD}=\widehat{HAD}\)

Do đó: ΔABD=ΔAHD

b: Ta có: ΔABD=ΔAHD

=>AB=AH và DB=DH

Ta có: AB=AH

=>A nằm trên đường trung trực của BH(1)

Ta có: DB=DH

=>D nằm trên đường trung trực của BH(2)

Từ (1),(2) suy ra AD là đường trung trực của BH

c: Xét ΔDBI vuông tại B và ΔDHC vuông tại H có

DB=DH

\(\widehat{BDI}=\widehat{HDC}\)(hai góc đối đỉnh)

Do đó: ΔDBI=ΔDHC

=>DI=DC

=>ΔDIC cân tại D

d: Ta có: ΔDBI=ΔDHC

=>BI=HC

Xét ΔAIC có \(\dfrac{AB}{BI}=\dfrac{AH}{HC}\)

nên BH//CI

e: Ta có: AB+BI=AI

AH+HC=AC

mà AB=AH và BI=HC

nên AI=AC

=>A nằm trên đường trung trực của CI(3)

Ta có: DI=DC

=>D nằm trên đường trung trực của CI(4)

Từ (3) và (4) suy ra AD là đường trung trực của CI

=>AD\(\perp\)CI

a: ta có: \(AE=EB=\dfrac{AB}{2}\)

\(AD=DC=\dfrac{AC}{2}\)

mà AB=AC

nên AE=EB=AD=DC

Xét ΔEBC và ΔDCB có

EB=DC

\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)

BC chung

Do đó: ΔEBC=ΔDCB

=>BD=CE

b: Ta có: ΔEBC=ΔDCB

=>\(\widehat{ECB}=\widehat{DBC}\)

=>\(\widehat{GBC}=\widehat{GCB}\)

=>ΔGBC cân tại G

c: Xét ΔABC có

BD,CE là các đường trung tuyến

BD cắt CE tại G

Do đó: G là trọng tâm của ΔABC

=>\(BG=\dfrac{2}{3}BD;CG=\dfrac{2}{3}CE\)

Vì \(BG=\dfrac{2}{3}BD\)

nên \(DG=\dfrac{1}{2}BG\)

Vì \(CG=\dfrac{2}{3}CE\)

nên \(EG=\dfrac{1}{2}CG\)

Xét ΔGBC có GB+GC>BC

=>\(2\left(EG+GD\right)>BC\)

=>\(GE+GD>\dfrac{BC}{2}\)

a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Xét ∆ABD và ∆ACD có:

AB = AC (gt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

b) Do ∠BAD = ∠CAD (cmt)

⇒ ∠EAD = ∠FAD

Xét hai tam giác vuông: ∆ADE và ∆ADF có:

AD là cạnh chung

∠EAD = ∠FAD (cmt)

⇒ ∆ADE = ∆ADF (cạnh huyền - góc nhọn)

⇒ DE = DF (hai cạnh tương ứng)

c) Do ∆ADE = ∆ADF (cmt)

⇒ AE = AF (hai cạnh tương ứng)

⇒ A nằm trên đường trung trực của EF (1)

Do DE = DF (cmt)

⇒ D nằm trên đường trung trực của EF (2)

Từ (1) và (2) ⇒ AD là đường trung trực của EF

⇒ AD ⊥ EF (*)

∆ABC có AB = AC (gt)

⇒ ∆ABC cân tại A

Mà AD là tia phân giác của ∠BAC

⇒ AD là đường trung trực của ∆ABC

⇒ AD ⊥ BC (**)

Từ (*) và (**) ⇒ EF // BC

c.

Từ câu a ta suy ra \(BD=CD\)

Xét hai tam giác vuông BDE và CDF có:

\(\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\\BD=CD\end{matrix}\right.\)  \(\Rightarrow\Delta_{\perp}BDE=\Delta_{\perp}CDF\left(ch-gn\right)\)

\(\Rightarrow BE=CF\)

Mà \(AB=AC\left(gt\right)\Rightarrow AE+BE=AF+CF\)

\(\Rightarrow AE=AF\) (1)

Theo cm câu b ta có \(DE=DF\) (2)

(1);(2) \(\Rightarrow AD\) là trung trực của EF

\(\Rightarrow AD\perp EF\)

\(\Rightarrow EF||BC\) (cùng vuông góc AD)