\(c,10x=15y=21zvà3x-7y+5z=30\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ac=b^2\)
=>\(\dfrac{a}{b}=\dfrac{b}{c}\)
\(bd=c^2\)
=>\(\dfrac{b}{c}=\dfrac{c}{d}\)
=>\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^3\end{matrix}\right.\)
\(\left(\dfrac{2a+3b-c}{2b+3c-d}\right)^3=\left(\dfrac{2\cdot dk^3+3\cdot dk^2-dk}{2\cdot dk^2+3\cdot dk-d}\right)^3\)
\(=\left(\dfrac{dk\left(2k^2+3k-1\right)}{d\left(2k^2+3k-1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{2a+3b-c}{2b+3c-d}\right)^3\)

Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{1}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}x=a\left(x+y+z\right)\\y=b\left(x+y+z\right)\\z=c\left(x+y+z\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=a^2\left(x+y+z\right)^2\\y^2=b^2\left(x+y+z\right)^2\\z^2=c^2\left(x+y+z\right)^2\end{matrix}\right.\)
\(\Rightarrow x^2+y^2+z^2=a^2\left(x+y+z\right)^2+b^2\left(x+y+z\right)^2+c^2\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=\left(a^2+b^2+c^2\right)\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=1.\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=\left(x+y+z\right)^2\)

a)
\(P\left(x\right)=6x^4+2x+4x^3-3x^2-10+x^3+3x\)
\(=6x^4+\left(4x^3+x^3\right)-3x^2+\left(2x+3x\right)-10\)
\(=6x^4+5x^3-3x^2+5x-10\)
\(Q\left(x\right)=4-5x^3+2x^2-x^3+5x^4+11x^3-4x\)
\(=5x^4+\left(-5x^3-x^3+11x^3\right)+2x^2-4x+4\)
\(=5x^4+5x^3+2x^2-4x+4\)
b)
\(P\left(x\right)+Q\left(x\right)\)
\(=\left(6x^4+5x^3-3x^2+5x-10\right)+\left(5x^4+5x^3+2x^2-4x+4\right)\)
\(=6x^4+5x^3-3x^2+5x-10+5x^4+5x^3+2x^2-4x+4\)
\(=\left(6x^4+5x^4\right)+\left(5x^3+5x^3\right)+\left(-3x^2+2x^2\right)+\left(5x-4x\right)+\left(-10+4\right)\)
\(=11x^4+10x^3-x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\)
\(=\left(6x^4+5x^3-3x^2+5x-10\right)-\left(5x^4+5x^3+2x^2-4x+4\right)\)
\(=6x^4+5x^3-3x^2+5x-10-5x^4-5x^3-2x^2+4x-4\)
\(=\left(6x^4-5x^4\right)+\left(5x^3-5x^3\right)+\left(-3x^2-2x^2\right)+\left(5x+4x\right)+\left(-10-4\right)\)
\(=x^4-5x^2+9x-14\)

Gọi x (ngày) là số ngày 12 công nhân đóng xong chiếc tàu (x > 0)
Do số công nhân có năng suất làm như nhau và cùng đóng một chiếc tàu nên số công nhân và số ngày đóng xong chiếc tàu là hai đại lượng tỉ lệ nghịch
⇒ x.12 = 20.60
x.12 = 1200
x = 1200 : 12
x = 100 (nhận)
Vậy 12 công nhân đóng xong chiếc tàu trong 100 ngày
Gọi x (ngày) là số ngày 12 công nhân đóng xong chiếc tàu (x > 0)
Do số công nhân có năng suất làm như nhau và cùng đóng một chiếc tàu nên số công nhân và số ngày đóng xong chiếc tàu là hai đại lượng tỉ lệ nghịch
⇒ x.12 = 20.60
x.12 = 1200
x = 1200 : 12
x = 100 (nhận)
Vậy 12 công nhân đóng xong chiếc tàu trong 100 ngày

Gọi x (giờ) là số giờ 15 người làm cỏ xong cánh đồng (x > 0)
Do số người có cùng năng suất và cùng làm cỏ một cánh đồng nên số người và số giờ làm cỏ xong cánh đồng là hai đại lượng tỉ lệ nghịch
⇒ x.15 = 10.3
x.15 = 30
x = 30 : 15
x = 2 (nhận)
Vậy 15 người làm cỏ cánh đồng đó xong trong 2 giờ
15 người sẽ làm cỏ cánh đồng đó xong trong:
\(10\cdot3:15=2\left(giờ\right)\)

Sửa đề: x=1 là nghiệm của P(x)
\(P\left(1\right)=a\cdot1^2+b\cdot1+c=a+b+c=0\)
=>x=1 là nghiệm của P(x) khi a+b+c=0

Ta có: DI//AB
=>\(\widehat{DIA}=\widehat{IAB}\)(hai góc so le trong)
mà \(\widehat{IAB}=\widehat{DAI}\)(AI là phân giác của góc DAB)
nên \(\widehat{DIA}=\widehat{DAI}\)
=>DI=DA
Ta có: DI//AB
=>\(\widehat{EIB}=\widehat{IBA}\)(hai góc so le trong)
mà \(\widehat{IBA}=\widehat{EBI}\)(BI là phân giác của góc EBA)
nên \(\widehat{EIB}=\widehat{EBI}\)
=>EB=EI
Ta có: DE=DI+IE
mà DI=DA và EB=EI
nên DE=DA+EB

Lời giải:
Áp dụng TCDTSBN:
$\frac{1}{x+y+z}=\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=\frac{y+z+1+x+z+2+y+x-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$
$\Rightarrow x+y+z=0,5$
Có:
$\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=2$
$\Rightarrow \frac{y+z+1}{x}+1=\frac{x+z+2}{y}+1=\frac{y+x-3}{z}+1=3$
$\Rightarrow \frac{x+y+z+1}{x}=\frac{x+y+z+2}{y}=\frac{x+y+z-3}{z}=3$
$\Rightarrow \frac{1,5}{x}=\frac{2,5}{y}=\frac{-2,5}{z}=3$
$\Rightarrow x=0,5; y=\frac{5}{6}; z=\frac{-5}{6}$

\(A=\dfrac{2x^2-4x+9}{2x^2-4x+7}\)
\(=\dfrac{2x^2-4x+7+2}{2x^2-4x+7}\)
\(=1+\dfrac{2}{2x^2-4x+7}\)
\(=1+\dfrac{2}{2x^2-4x+2+5}\)
\(=1+\dfrac{2}{2\left(x-1\right)^2+5}\)
Vì \(2\left(x-1\right)^2+5>=5\forall x\)
nên \(\dfrac{2}{2\left(x-1\right)^2+5}< =\dfrac{2}{5}\forall x\)
=>\(1+\dfrac{2}{2\left(x-1\right)^2+5}< =\dfrac{2}{5}+1=\dfrac{7}{5}\forall x\)
Dấu '=' xảy ra khi x=1
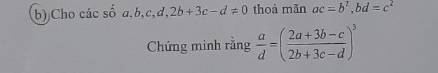
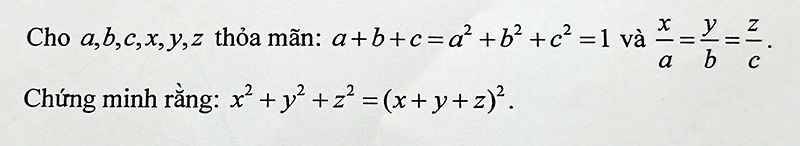

10x=15y=21z
=>\(\dfrac{10x}{210}=\dfrac{15y}{210}=\dfrac{21z}{210}\)
=>\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
mà 3x-7y+5z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=\dfrac{3x-7y+5z}{3\cdot21-7\cdot14+5\cdot10}=\dfrac{30}{15}=2\)
=>\(x=2\cdot21=42;y=2\cdot14=28;z=2\cdot10=20\)
\(10x=15y=21z\Rightarrow\dfrac{10x}{210}=\dfrac{15y}{210}=\dfrac{21z}{210}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}=\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=21.2=42\\y=14.2=28\\z=10.2=20\end{matrix}\right.\)