cho nửa đường tròn (O) , đường kính AB vẽ tiếp tuyến Ax lấy M thuộc Ax từ M vẽ tiếp tuyến MC ( C thuộc (O)). Gọi I là giao điểm của OM và AC, Q là giao điểm của MB và (O). C/m:
a tg AIQM nội tiếp đường tròn
b góc ABM=góc MIQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
YN
16 tháng 2 2023
A C H P I B M K O (hình minh họa)
Xét tứ giác AIHK:
\(\widehat{AIH}+\widehat{AKH}=90^o+90^o=180^o\)
\(\Rightarrow\) Tứ giác AIHK nội tiếp
Xét \(\Delta MIB\) và \(\Delta MCK\):
\(\widehat{IMC}\) chung
\(\widehat{MBI}=\widehat{MKC}\)
\(\Rightarrow\Delta MIB~\Delta MCK\left(g.g\right)\)
\(\Rightarrow\dfrac{MI}{MB}=\dfrac{MC}{MK}\)
\(\Leftrightarrow MI.MK=MC.MB\)
\(\widehat{IMP}=\dfrac{1}{2}\widehat{IMB}\)
\(\widehat{IAP}=\dfrac{1}{2}\widehat{IAK}\)
\(\Rightarrow\widehat{APM}=180^o-\dfrac{1}{2}\left(\widehat{IMB}+\widehat{IAK}\right)=180^o-\dfrac{1}{2}.180^o=90^o\)
\(\Rightarrow AP\perp MP\).
15 tháng 2 2023
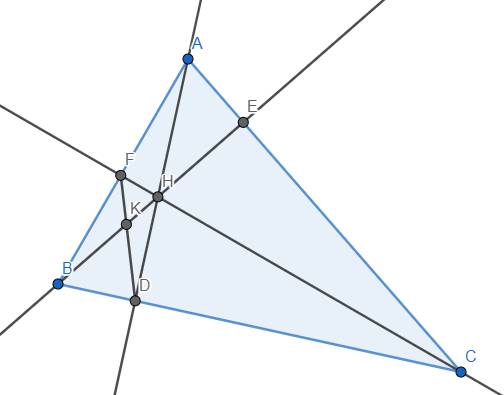
a) Dễ thấy \(\widehat{ADC}=\widehat{AFC}=90^o\) \(\Rightarrow\) Tứ giác ACDF nội tiếp đường tròn nhận AC làm đường kính \(\Rightarrow\) Tâm của đường tròn ngoại tiếp tứ giác ACDF chính là trung điểm của đoạn AC.
b) Áp dụng định lý Menelaus cho tam giác HBC với cát tuyến DFK, ta có \(\dfrac{KH}{KB}.\dfrac{DB}{DC}.\dfrac{FC}{FH}=1\) \(\Rightarrow\dfrac{KH}{KB}=\dfrac{DC}{DB}.\dfrac{FH}{FC}\) (1)
Áp dụng định lý Ceva cho tam giác HBC với các đường đồng quy CE, DH, BF và \(D\in BC,E\in HB,F\in HC\), ta có \(\dfrac{DC}{DB}.\dfrac{EB}{EH}.\dfrac{FH}{FC}=1\) \(\Rightarrow\dfrac{EH}{EB}=\dfrac{DC}{DB}.\dfrac{FH}{FC}\) (2)
Từ (1) và (2) suy ra \(\dfrac{KH}{KB}=\dfrac{EH}{EB}\) \(\Rightarrow\) đpcm
14 tháng 2 2023
Nếu bạn chưa thấy câu trả lời thì vào trang cá nhân của mình xem nhé.
G
2
12 tháng 2 2023
\(DKXD:a\ne0\)
\(\dfrac{x-a}{3}\text{=}\dfrac{x+3}{a}+2\)
\(\Leftrightarrow\dfrac{a\left(x-a\right)}{3a}\text{=}\dfrac{3\left(x+3\right)}{3a}-\dfrac{6a}{3a}\)
\(\Rightarrow a\left(x-a\right)\text{=}3\left(x+3\right)-6a\)
\(\Leftrightarrow ax-a^2\text{=}3x+9-6a\)
\(\Leftrightarrow ax-3x\text{=}a^2-6a+9\)
\(\Leftrightarrow x\left(a-3\right)\text{=}\left(a-3\right)^2\)
Nếu \(a\ne3\) , phương trình có nghiệm \(x\text{=}a-3\)
Nếu \(a\text{=}3\) thì pt có dạng : \(0x\text{=}0\)
\(Vay...\)
12 tháng 2 2023
cái chỗ : \(0x\text{=}0\left(ptvonghiem\right)\) rồi kết luận nha