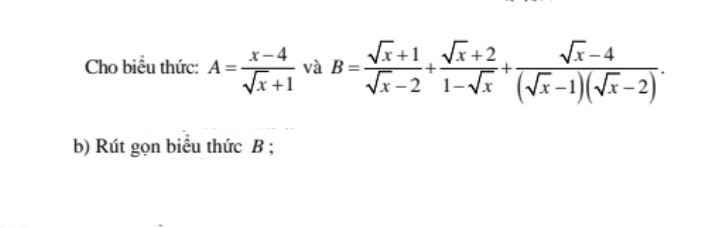b) Xét phương trình 2 có 
(1-x² )/(1+xy)² - (x+y)²    - y² =1
=>(1-x²)/1+2xy+x²y²-x²-2xy-y²   -y²=1
=>(1-x²) /(1-x² )-y²(1-x²)       -y² =1
=>(1-x²)/(1-x²)(1-y²)       -y²=1
=>1/(1-y²)    -y²=1
=>1=(1-y²)²
=>1=1-2y²+y4
=>y⁴-2y²=0
=>y²(y²-2)=0
=>y=0
y²-2=0
=> y=+√2
=> y=-√2
 Thay y vào phương trình 1 là ra x 

à nhầm ... sửa lại dòng 6 
=> 1/(1-y²) - y²=1
=> 1/(1-y²)=1+y²
=> 1=1-y⁴
=> y=0
=>x=3
=> x=-3
 

Lời giải:

Áp dụng BĐT Cauchy-Schwarz và AM-GM:

$M=\frac{b^2+c^2}{a^2}+a^2(\frac{1}{b^2}+\frac{1}{c^2})$

$\geq \frac{b^2+c^2}{a^2}+a^2.\frac{4}{b^2+c^2}$

$=(\frac{b^2+c^2}{a^2}+\frac{a^2}{b^2+c^2})+\frac{3a^2}{b^2+c^2}$

$\geq \sqrt{\frac{b^2+c^2}{a^2}.\frac{a^2}{b^2+c^2}}+\frac{3(b^2+c^2)}{b^2+c^2}$

$=2+3=5$

Vậy $M_{\min}=5$ 

Với mọi a,b∈Z+�,�∈�+ ta có: (a+b)2≤2(a2+b2)(�+�)2≤2(�2+�2) ⇔n4≤2(n3+2)⇔�4≤2(�3+2)

 ⇔n4−2n3−4≤0⇔n3(n−2)−4≤0(∗)⇔�4−2�3−4≤0⇔�3(�−2)−4≤0(∗)

+) Nếu n≥3�≥3 thì n3(n−2)−4≥n3−4>0�3(�−2)−4≥�3−4>0 (mâu thuẫn với (*))

⇒n∈{0;1;2}⇒�∈{0;1;2}

+) Với n=0⇒{a+b=0a2+b2=2⇒�=0⇒{�+�=0�2+�2=2⇒ không tồn tại a,b∈Z+�,�∈�+ thỏa mãn hệ phương trình.

+) Với n=1⇒{a+b=1a2+b2=3⇒�=1⇒{�+�=1�2+�2=3⇒ không tồn tại a,b∈Z+�,�∈�+ thỏa mãn hệ phương trình.

+) Với n=2⇒{a+b=4a2+b2=10⇔{a+b=4(a+b)2−2ab=10⇔{a+b=4ab=3�=2⇒{�+�=4�2+�2=10⇔{�+�=4(�+�)2−2��=10⇔{�+�=4��=3

Khi đó ta có hai số a,b�,� là nghiệm của phương trình: x2−4x+3=0⇔[x=1x=3�2−4�+3=0⇔[�=1�=3

⇒(a;b)∈{(1;3);(3;1)}.⇒(�;�)∈{(1;3);(3;1)}.

Vậy nghiệm của hệ phương trình đã cho là: (n;a;b)∈{(2;1;3);(2;3;1)}(�;�;�)∈{(2;1;3);(2;3;1)}

nếu đúng cho mình xin 1 tick nhé!!!!

 Trước hết, ta đi chứng minh một bổ đề sau: Nếu \(a+b+c=0\) thì \(a^3+b^3+c^3=3abc\). Thật vậy, ta phân tích 

 \(P=a^3+b^3+c^3-3abc\)

\(P=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)

\(P=\left(a+b+c\right)\left[\left(a+b\right)^2+\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)\)

\(P=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\).

Hiển nhiên nếu \(a+b+c=0\) thì \(P=0\) hay \(a^3+b^3+c^3=3abc\), bổ đề được chứng minh.

Do \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\) nên áp dụng bổ đề, ta được \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\).

Vì vậy \(\dfrac{yz}{x^2}+\dfrac{zx}{y^2}+\dfrac{xy}{z^2}=\dfrac{xyz}{x^3}+\dfrac{xyz}{y^3}+\dfrac{xyz}{z^3}\) \(=xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)\) \(=xyz.\dfrac{3}{xyz}=3\). Ta có đpcm

 Chỗ kia chắc là \(n\) điểm chứ không phải \(n+1\) đâu.

 Giả sử \(n\) điểm đã cho không thẳng hàng. Gọi S là tập hợp gồm \(n\) điểm đã cho và \(T=\left\{\left(A,B,C\right):A,B,C\in S|d\left(A,BC\right)>0\right\}\). 

 Vì n điểm đã cho không thẳng hàng nên \(T\ne\varnothing\). Mà T là có hữu hạn phần tử nên tồn tại phần tử \(\left(A,B,C\right)\in T\) sao cho \(d\left(A,BC\right)\) nhỏ nhất.

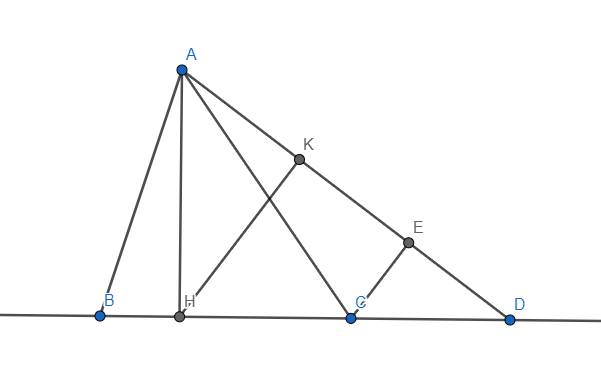
 Theo giả thiết thì đường thẳng BC còn đi qua 1 điểm thứ ba nữa là \(D\in S\) . Không mất tính tổng quát, giả sử C nằm giữa B và D. Hạ \(AH\perp BC\), \(HK\perp AD\) và \(CE\perp AD\). Ta có \(CE< HK< AH\). Suy ra phần tử \(\left(C,A,D\right)\in T\) có \(d\left(C,AD\right)< d\left(A,BC\right)\), điều này là vô lí vì ta đã giả sử phần tử \(\left(A,B,C\right)\in T\) có \(d\left(A,BC\right)\) nhỏ nhất.

 Vậy điều giả sử là sai, suy ra \(n\) điểm đã cho thẳng hàng.

Vẫn như lần trước nhé bạn. Nếu bạn không xem được câu trả lời trên đây thì vào trong trang cá nhân của mình xem nhé.

Áp dụng BĐT Bunhiacopxki:

\(\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ac+bc\right)^2}=ac+bc\)

CMTT : \(\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ad+bd\)

Ta có :\(\sqrt{\left(a^2+c^2\right)\left(b^2+c^2\right)}+\sqrt{\left(a^2+d^2\right)\left(b^2+d^2\right)}\ge ac+bc+ad+bd=\left(a+b\right)\left(c+d\right)\)

Áp dụng BĐT Bunhiacopxki:

(�2+�2)(�2+�2)≥(��+��)2=��+��(a2+c2)(b2+c2)​≥(ac+bc)2​=ac+bc

CMTT : (�2+�2)(�2+�2)≥��+��(a2+d2)(b2+d2)​≥ad+bd

Ta có :(�2+�2)(�2+�2)+(�2+�2)(�2+�2)≥��+��+��+��=(�+�)(�+�)(a2+c2)(b2+c2)​+(a2+d2)(b2+d2)​≥ac+bc+ad+bd=(a+b)(c+d)

Áp dụng BĐT Bunhiacopxki :

(a² + b² + c²)² = (1.a² + 1.b² + 1.c²)

≤ (1² + 1² + 1²)[ (a²)² + (b²)² + (c²)² ]

= 3(a⁴ + b⁴ + c⁴)

⇒ n = 3

Dễ thấy \(\widehat{BAH}=90^o-\widehat{B}=\widehat{C}\), mà \(\widehat{C}=30^o\) nên \(\widehat{BAH}=30^o\). Trong tam giác ABH vuông tại H, ta có \(\dfrac{BH}{AH}=\tan\widehat{BAH}=\tan30^o=\dfrac{\sqrt{3}}{3}\).

Trước hết ta tính \(\dfrac{S_{BHE}}{S_{ABH}}\). Để ý rằng \(\dfrac{S_{BHE}}{S_{ABH}}=\dfrac{EH}{AH}\). Mặt khác, \(\dfrac{EH}{AE}=\dfrac{BH}{AB}=\sin\widehat{BAH}=\sin30^o=\dfrac{1}{2}\) \(\Rightarrow\dfrac{EH}{AH}=\dfrac{1}{3}\) hay \(\dfrac{S_{BHE}}{S_{ABH}}=\dfrac{1}{3}\) (*). Lại thấy \(\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{BH}{BC}\), mà \(\dfrac{BH}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AB\) và \(\dfrac{AB}{BC}=\sin\widehat{C}=\sin30^o=\dfrac{1}{2}\) \(\Rightarrow AB=\dfrac{1}{2}BC\). Từ đó suy ra \(BH=\dfrac{1}{4}BC\) hay \(\dfrac{BH}{BC}=\dfrac{1}{4}\) hay \(\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{1}{4}\) (**)

Từ (*) và (**) \(\Rightarrow\dfrac{S_{BHE}}{S_{ABH}}.\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{1}{3}.\dfrac{1}{4}\Rightarrow\dfrac{S_{BHE}}{S_{ABC}}=\dfrac{1}{12}\)

\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{1-\sqrt{x}}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\left(x\ge1\right)\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{x-1-\left(x-4\right)+\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{x-1-x+4+\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{1}{\sqrt{x}-2}\)