
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)
⇔ m.|- \(\dfrac{1}{2}\)| + 2.(-\(\dfrac{1}{2}\)) = 1
\(\dfrac{1}{2}\)m - 1 = 1
\(\dfrac{1}{2}\)m = 2
m = 2 x 2
m = 4
Kết luận với m = 4 thì đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)

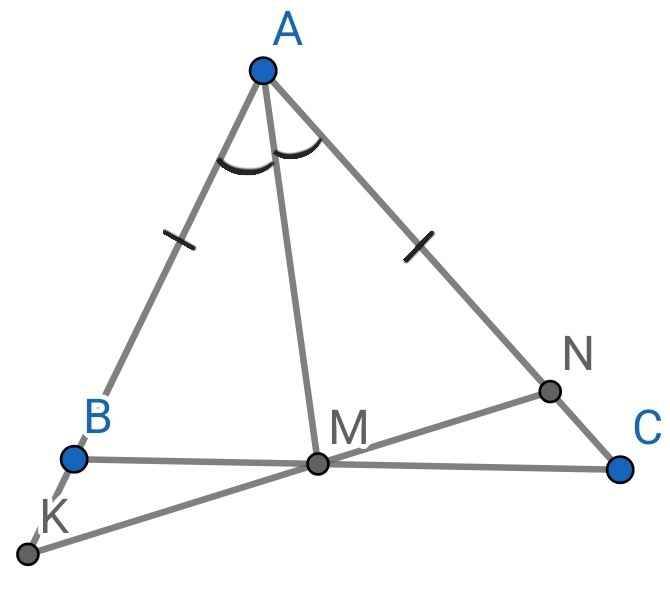
Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
⇒ ∠BAM = ∠NAM
Xét ∆ABM và ∆ANM có:
AB = AN (gt)
∠BAM = ∠NAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ANM (c-g-c)
⇒ MB = MN (hai cạnh tương ứng)

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-65^0=115^0\)
=>\(\widehat{IBC}+\widehat{ICB}=57,5^0\)
Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
=>\(\widehat{BIC}=180^0-57,5^0=122,5^0\)

a: Ta có: \(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔADB và ΔAEC có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>BD=CE
b: Ta có: ΔADB=ΔAEC
=>AD=AE
=>ΔADE cân tại A
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
nên ED//BC

a: Ta có: \(DM=MF=\dfrac{DF}{2}\)
\(DN=NE=\dfrac{DE}{2}\)
mà DF=DE
nên DM=MF=DN=NE
Xét ΔDEM và ΔDFN có
DE=DF
\(\widehat{EDM}\) chung
DM=DN
Do đó: ΔDEM=ΔDFN
=>EM=FN và \(\widehat{DEM}=\widehat{DFN}\)
b: Xét ΔNEF và ΔMFE có
NE=MF
\(\widehat{NEF}=\widehat{MFE}\)
EF chung
Do đó: ΔNEF=ΔMFE
=>\(\widehat{NFE}=\widehat{MEF}\)
=>\(\widehat{KEF}=\widehat{KFE}\)
=>KE=KF
c: Ta có: ΔDEF cân tại D
mà DH là đường cao
nên H là trung điểm của EF
Xét ΔDEF có
DH,EM,FN là các đường trung tuyến
Do đó: DH,EM,FN đồng quy

a: Xét ΔEDN và ΔEFN có
ED=EF
\(\widehat{DEN}=\widehat{FEN}\)
EN chung
Do đó: ΔEDN=ΔEFN
=>ND=NF
=>ΔNDF cân tại N
b: ΔEDN=ΔEFN
=>\(\widehat{EDN}=\widehat{EFN}\)
=>\(\widehat{EFN}=90^0\)
=>NF\(\perp\)FE

a: Xét ΔADB vuông tại D và ΔADE vuông tại D có
AD chung
DB=DE
Do đó: ΔADB=ΔADE
=>AB=AE
=>ΔABE cân tại A
b: Gọi H là giao điểm của CK và AD
Xét ΔAHC có
CD,AK là các đường cao
CD cắt AK tại E
Do đó: E là trực tâm của ΔAHC
=>HE\(\perp\)AC
mà EF\(\perp\)AC
nên H,E,F thẳng hàng
=>AD,EF,CK đồng quy

a: Xét ΔDKE và ΔDHF có
DK=DH
\(\widehat{KDE}\) chung
DE=DF
Do đó: ΔDKE=ΔDHF
=>KE=HF
b: Ta có: ΔDKE=ΔDHF
=>\(\widehat{DHF}=\widehat{DKE};\widehat{DEK}=\widehat{DFH}\)
Ta có: \(\widehat{DHF}+\widehat{EHF}=180^0\)(hai góc kề bù)
\(\widehat{DKE}+\widehat{FKE}=180^0\)(hai góc kề bù)
mà \(\widehat{DHF}=\widehat{DKE}\)
nên \(\widehat{EHF}=\widehat{FKE}\)
Ta có: DH+HE=DE
DK+KF=DF
mà DH=DK và DE=DF
nên HE=KF
Xét ΔOHE và ΔOKF có
\(\widehat{OHE}=\widehat{OKF}\)
HE=KF
\(\widehat{OEH}=\widehat{OFK}\)
Do đó: ΔOHE=ΔOKF
c: Ta có: ΔOHE=ΔOKF
=>OE=OF
=>O nằm trên đường trung trực của EF(1)
Ta có: DE=DF
=>D nằm trên đường trung trực của EF(2)
Từ (1),(2) suy ra DO là đường trung trực của EF
=>DO\(\perp\)EF

\(\dfrac{x^5+5x^3-3x^4-2x^2+3x-6}{x^2-3x+5}\)
\(=\dfrac{x^5-3x^4+5x^3-2x^2+6x-10-3x+4}{x^2-3x+5}\)
\(=\dfrac{x^3\left(x^2-3x+5\right)-2\left(x^2-3x+5\right)-3x+4}{x^2-3x+5}\)
\(=x^3-2+\dfrac{-3x+4}{x^2-3x+5}\)







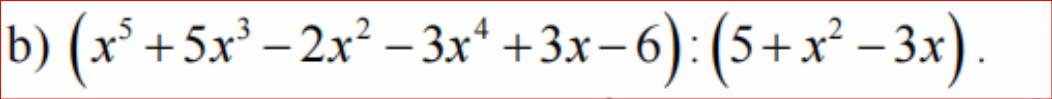
a: M là trung điểm của BC
=>\(BM=CM=\dfrac{BC}{2}\)
mà BA=BC/2
nên BM=CM=BA
Xét ΔBAD và ΔBMD có
BA=BM
\(\widehat{ABD}=\widehat{MBD}\)
BD chung
Do đó: ΔBAD=ΔBMD
b: ta có; ΔBAD=ΔBMD
=>\(\widehat{BAD}=\widehat{BMD}\)
Xét ΔBAC và ΔBME có
\(\widehat{BAC}=\widehat{BME}\)
BA=BM
\(\widehat{ABC}\) chung
Do đó: ΔBAC=ΔBME
=>BE=BC
=>ΔBEC cân tại B
Ta có: ΔBEC cân tại B
mà BD là đường phân giác
nên DB là đường trung tuyến
=>N là trung điểm của EC
Xét ΔEBC có
BN,EM là các đường trung tuyến
BN cắt EM tại D
Do đó: D là trọng tâm của ΔEBC
=>BD/DN=2