Lời giải:

$|x-2023|=x-2023$

$\Rightarrow x-2023\geq 0$

$\Rightarrow x\geq 2023$.

x thỏa mãn tất cả các GT .

Lời giải:

$2xy=x+y$

$\Rightarrow 2xy-x-y=0$

$\Rightarrow x(2y-1)-y=0$

$\Rightarrow 2x(2y-1)-2y=0$

$\Rightarrow 2x(2y-1)-(2y-1)=1$

$\Rightarrow (2x-1)(2y-1)=1$

Do $x,y$ nguyên nên $2x-1,2y-1$ nguyên. Mà tích của chúng bằng $1$ nên ta xét các TH sau:

TH1: $2x-1=1, 2y-1=1\Rightarrow x=y=1$

TH2: $2x-1=-1, 2y-1=-1\Rightarrow x=y=0$

Vậy........

Lời giải:

a.

$(4x^4+3x^3):(-x^3)+(15x^2+6x):3x=0$

$\Rightarrow -4x-3+(5x+2)=0$

$\Rightarrow -4x-3+5x+2=0$

$\Rightarrow x-1=0$

$\Rightarrow x=1$
b.

$(x^2-\frac{1}{2}x):(2x)-(3x-1)^2:(3x-1)=0$

$\Rightarrow \frac{x}{2}-\frac{1}{4}-(3x-1)=0$

$\Rightarrow \frac{x}{2}-\frac{1}{4}-3x+1=0$

$\Rightarrow \frac{-5}{2}x+\frac{3}{4}=0$

$\Rightarrow \frac{-5}{2}x=\frac{-3}{4}$

$\Rightarrow x=\frac{3}{10}$

a: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)

=>\(-4x-3+5x+2=0\)

=>x-1=0

=>x=1

b: \(\left(x^2-\dfrac{1}{2}x\right):2x-\left(3x-1\right)^2:\left(3x-1\right)=0\)

=>\(\dfrac{1}{2}x-\dfrac{1}{4}-\left(3x-1\right)=0\)

=>\(\dfrac{1}{2}x-\dfrac{1}{4}-3x+1=0\)

=>\(-\dfrac{5}{2}x=\dfrac{1}{4}-1=-\dfrac{3}{4}\)

=>\(x=\dfrac{3}{4}:\dfrac{5}{2}=\dfrac{3}{4}\cdot\dfrac{2}{5}=\dfrac{6}{20}=\dfrac{3}{10}\)

Bài 4

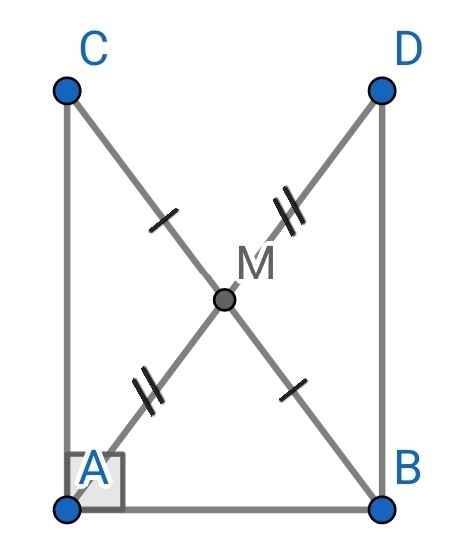
a) Do AM là đường trung tuyến của ∆ABC (gt)

⇒ M là trung điểm của BC

⇒ BM = CM

Xét ∆AMC và ∆DMB có:

AM = DM (gt)

∠AMC = ∠DMB (đối đỉnh)

CM = BM (cmt)

⇒ ∆AMC = ∆DMB (c-g-c)

⇒ ∠ACM = ∠DBM (hai góc tương ứng)

Mà ∠ACM và ∠DBM là hai góc so le trong

⇒ AC // BD

Mà AC ⊥ AB (do ∆ABC vuông tại A)

⇒ BD ⊥ AB

⇒ ∠ABD = 90⁰

b) Do ∆AMC = ∆DMB (cmt)

⇒ AC = DB (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆ABC và ∆BAD có:

AB là cạnh chung

AC = BD (cmt)

⇒ ∆ABC = ∆BAD (hai cạnh góc vuông)

c) Do ∆ABC = ∆BAD (cmt)

⇒ BC = AD (hai cạnh tương ứng)

Lại có:

AM = MD (gt)

⇒ M là trung điểm của AD

⇒ AM = AD : 2

Mà AD = BC (cmt)

⇒ AM = BC : 2

Bài 1

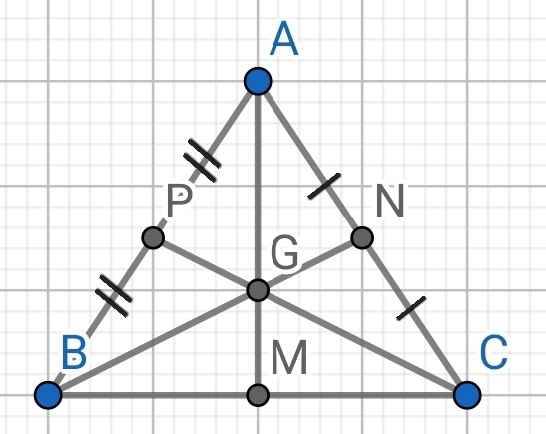
a) Do BN và CP là hai đường trung tuyến của ABC (gt)

G là giao điểm của BN và CP (gt)

⇒ G là trọng tâm của ABC

⇒ AG là đường trung tuyến của ABC

⇒ AM là đường trung tuyến của ABC

b) Do ABC cân tại A (gt)

⇒ AB = AC

Do AM là đường trung tuyến của ∆ABC (cmt)

⇒ M là trung điểm của BC

⇒ BM = CM

Xét ∆AMB và ∆AMC có:

AB = AC (cmt)

BM = CM (cmt)

AM là cạnh chung

⇒ ∆AMB = ∆AMC (c-c-c)

c) Do ∆AMB = ∆AMC (cmt)

⇒ ∠BAM = ∠CAM (hai góc tương ứng)

⇒ AM là tia phân giác của ∠BAC

d) Do AB = AC (cmt)

⇒ A nằm trên đường trung trực của BC (1)

Do BM = CM (cmt)

⇒ M nằm trên đường trung trực của BC (2)

Từ (1) và (2) ⇒ AM là đường trung trực của BC

e) Do ∆ABC cân tại A (gt)

⇒ ∠ABC = ∠ACB

⇒ ∠PBC = ∠NCB

Do CP là đường trung tuyến của ∆ABC (gt)

⇒ P là trung điểm của AB

⇒ BP = AB : 2

Do BN là đường trung tuyến của ∆ABC (gt)

⇒ N là trung điểm của AC

⇒ CN = AC : 2

Mà AB = AC

⇒ BP = CN

Xét ∆PBC và ∆NCB có:

BP = CN (cmt)

∠PBC = ∠NCB (cmt)

BC là cạnh chung

⇒ ∆PBC = ∆NCB (c-g-c)

⇒ CP = BN (hai cạnh tương ứng)

Hay BN = CP

a:

Sửa đề: MN<MP; MQ là phân giác

Xét ΔMNQ và ΔMEQ có

MN=ME

\(\widehat{NMQ}=\widehat{EMQ}\)

MQ chung

Do đó: ΔMNQ=ΔMEQ

=>NQ=EQ

b: ΔMNQ=ΔMEQ

=>\(\widehat{MNQ}=\widehat{MEQ}\)

Xét ΔMEH và ΔMNP có

\(\widehat{EMN}\) chung

ME=MN

\(\widehat{MEH}=\widehat{MNP}\)

Do đó: ΔMEH=ΔMNP

c: Xét ΔMNP có MQ là phân giác

nên \(\dfrac{NQ}{NM}=\dfrac{QP}{MP}\)

mà MN<MP

nên NQ<QP

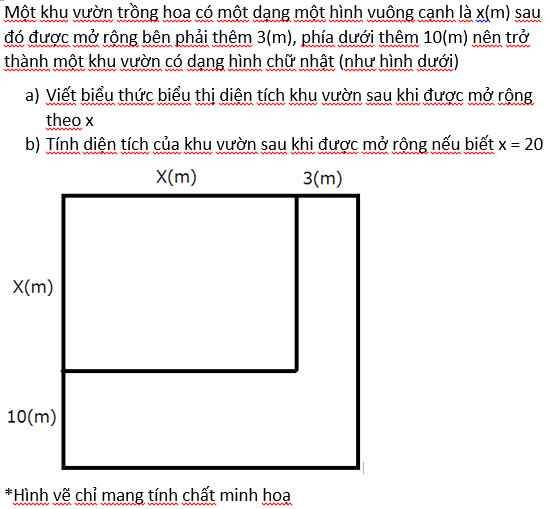
a: Chiều rộng khu vườn sau khi mở rộng là x+3(m)

Chiều dài khu vườn sau khi mở rộng là x+10(m)

Diện tích khu vườn sau khi mở rộng là:

\(S=\left(x+3\right)\left(x+10\right)=x^2+13x+30\)(m²)

b: Khi x=20 thì \(S=20^2+13\cdot20+30=690\left(m^2\right)\)

a:

1379m=1,379km

Độ dài quãng đường còn lại là x-1,379(km)

Số tiền phải trả cho x-1,379 km còn lại là:

14500(x-1,379)(đồng)

Tổng số tiền phải trả là:

20000+14500(x-1,379)(đồng)

b: Số tiền khách hàng phải trả nếu đi 15km là:

\(20000+14500\left(15-1,379\right)\simeq217505\left(đồng\right)\)

\(x\) < \(x\) là sao em?

2 < x < 20 cô ạ