\(BC^2=AB^2+AC^2\Rightarrow AC^2=BC^2-AB^2=2500-900=1600\left(Pitago\right)\)

\(\Rightarrow AC=40\left(cm\right)\)

\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{30.40}{50}=24\left(cm\right)\)

\(AB^2=AH^2+HB^2\Rightarrow HB^2=AB^2-AH^2=900-576=324\left(Pitago\right)\)

\(\Rightarrow HB=18\left(cm\right)\)

\(HC=BC-HB=50-18=32\left(cm\right)\)

đkxđ: \(x,y,z\ge2\)

Biến đổi pt đầu tiên, ta được:

\(x+y-2=4\sqrt{z-2}\)

\(\Leftrightarrow\left(x-2\right)+\left(y-2\right)=4\sqrt{z-2}-2\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x-2}=a\\\sqrt{y-2}=b\\\sqrt{z-2}=c\end{matrix}\right.\) với \(a,b,c\ge0\) thì ta thu được:

\(a^2+b^2=4c-2\)

Lập 2 đẳng thức tương tự rồi cộng theo vế, ta được:

\(2\left(a^2+b^2+c^2\right)=4\left(a+b+c\right)-6\)

\(\Leftrightarrow a^2+b^2+c^2+3=2a+2b+2c\) (*)

 Mà lại có \(a^2+1\ge2a\) \(\Rightarrow\) \(a^2+b^2+c^2+3\ge2a+2b+2c\)

 Nên để (*) xảy ra thì \(a=b=c=1\) \(\Leftrightarrow x=y=z=3\)

Vậy hpt đã cho có nghiệm \(\left(x,y,z\right)=\left(3,3,3\right)\)

Ta thấy \(2x^2< 4\) \(\Leftrightarrow x^2< 2\) \(\Leftrightarrow x^2=1\) (do \(x\ne0\))

Thế vào pt đề bài, ta có \(3+\dfrac{y^2}{4}=4\) 

\(\Leftrightarrow\dfrac{y^2}{4}=1\)

\(\Leftrightarrow y^2=4\)

\(\Leftrightarrow y=\pm2\)

Vậy, các cặp số (x; y) thỏa ycbt là \(\left(1;2\right);\left(-1;-2\right);\left(1;-2\right);\left(-1;2\right)\)

a

\(y^2+2xy-3x-2=0\)

\(\Leftrightarrow\left(y^2+2xy+x^2\right)-\left(x^2+3x+2\right)=0\)

\(\Leftrightarrow\left(x+y\right)^2=\left(x+1\right)\left(x+2\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+2=0\end{matrix}\right.\)

Nếu \(x+1=0\) thì \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\). 

Nếu \(x+2=0\) thì \(\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\)

Thử lại, ta thấy thỏa mãn. Vậy ta tìm được các cặp số \(\left(x;y\right)\) thỏa mãn đề bài là \(\left(-1;1\right),\left(-2;2\right)\)

\(x^2-25=y\left(y+6\right)\)

\(\Leftrightarrow x^2-25=y^2+6y\)

\(\Leftrightarrow x^2-25-y^2-6y=0\)

\(\Leftrightarrow x^2-\left(y^2+6y+9\right)-16=0\)

\(\Leftrightarrow x^2-\left(y+3\right)^2=16\)

\(\Leftrightarrow\left(x+y+3\right)\left(x-y-3\right)=16\)

\(\Leftrightarrow\left(x+y+3\right);\left(x-y-3\right)\in\left\{-1;1;-2;2;-4;4;-8;8;-16;16\right\}\)

Ta giải các hệ phương trình sau :

1) \(\left\{{}\begin{matrix}x+y+3=-1\\x-y-3=-16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-4\\x-y=-15\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x=-11\left(loại\right)\\x-y=-15\end{matrix}\right.\)

2) \(\left\{{}\begin{matrix}x+y+3=1\\x-y-3=16\end{matrix}\right.\)  \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-2\\x-y=19\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=17\left(loại\right)\\x-y=19\end{matrix}\right.\)

3) \(\left\{{}\begin{matrix}x+y+3=2\\x-y-3=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-1\\x-y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=10\\x-y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-6\end{matrix}\right.\)

4) \(\left\{{}\begin{matrix}x+y+3=-2\\x-y-3=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-5\\x-y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-10\\x-y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\)

5) \(\left\{{}\begin{matrix}x+y+3=-4\\x-y-3=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-7\\x-y=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-6\\x-y=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)

6) \(\left\{{}\begin{matrix}x+y+3=4\\x-y-3=4\end{matrix}\right.\)  \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x-y=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=8\\x-y=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-3\end{matrix}\right.\)

7) \(\left\{{}\begin{matrix}x+y+3=-8\\x-y-3=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-11\\x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-10\\x-y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=-6\end{matrix}\right.\)

8) \(\left\{{}\begin{matrix}x+y+3=8\\x-y-3=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\x-y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=10\\x-y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=0\end{matrix}\right.\)

9) \(\left\{{}\begin{matrix}x+y+3=-16\\x-y-3=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=-19\\x-y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=-17\left(loại\right)\\x-y=2\end{matrix}\right.\)

10) \(\left\{{}\begin{matrix}x+y+3=16\\x-y-3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=15\\x-y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=19\left(loại\right)\\x-y=4\end{matrix}\right.\)

Vậy \(\left(x;y\right)\in\left\{\left(5;-6\right);\left(-5;0\right);\left(-3;-2\right);\left(4;-3\right);\left(-5;-6\right);\left(5;0\right)\right\}\)

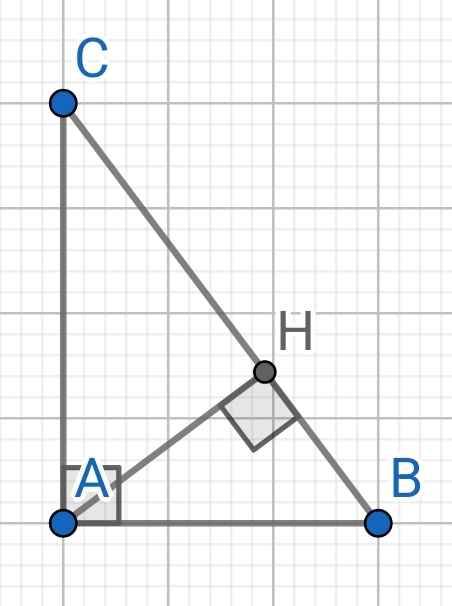 a) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AB² = BC.BH

⇒ BH = AB²/BC

= 6²/10

= 3,6 (cm)

⇒ HC = BC - BH

= 10 - 3,6

= 6,4 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AH.BC = AB.AC

⇒ AH = AB.AC/BC

= 6.8/10

= 4,8 (cm)

b) Ta có:

BC = BH + CH

= 12 + 27

= 29 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AB² = BC.BH

= 29.12

= 348

⇒ AB = 2√87

∆ABC vuông tại A, AH là đường cao

⇒ AC² = BC.CH

= 29.17

= 493

⇒ AC = √493 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AH² = BH.HC

= 12.17

= 204

⇒ AH = 2√51 (cm)