a) Ta có:

x² ≥ 0 với mọi x ∈ R

⇒ x² + 4 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

b) Ta có:

⇒ (x - 1)² ≥ 0 với mọi x ∈ R

≺ (x - 1)² + 7 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

c) x² + 2x + 2

= x² + x + x + 1 + 1

= (x² + x) + (x + 1) + 1

= x(x + 1) + (x + 1) + 1

= (x + 1)(x + 1) + 1

= (x + 1)² + 1

Ta có:

(x + 1)² ≥ 0 với mọi x ∈ R

⇒ (x + 1)² + 1 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

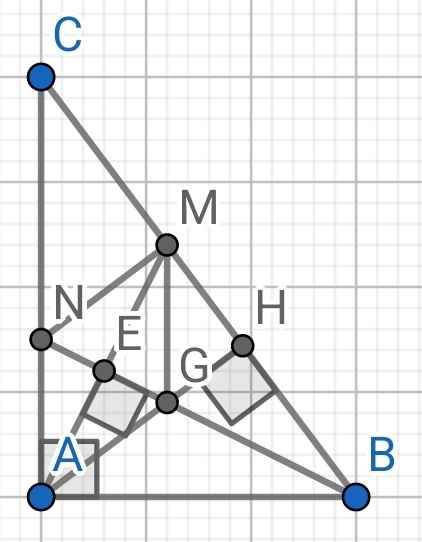
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:

BA = BM (gt)

BE là cạnh chung

⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)

b) Do ∆ABE = ∆MBE (cmt)

⇒ ∠ABE = ∠MBE (hai góc tương ứng)

⇒ ∠ABN = ∠MBN

Xét ∆ABN và ∆MBN có:

BA = BM (gt)

∠ABN = ∠MBN (cmt)

BN là cạnh chung

⇒ ∆ABN = ∆MBN (c-g-c)

⇒ AN = MN (hai cạnh tương ứng)

c) Do ∆ABN = ∆MBN (cmt)

⇒ ∠BAN = ∠BMN (hai góc tương ứng)

Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)

⇒ ∠BMN = 90⁰

⇒ MN ⊥ BM

⇒ MN ⊥ BC

Lại có AH là đường cao của ∆ABC (gt)

⇒ AH ⊥ BC

Mà MN ⊥ BC (cmt)

⇒ AH // MN

⇒ ∠MGN = ∠ANG (so le trong)

Cho tam giác ABC vuông tại A ( AB < AC ). Trên tia đối của tia AB, lấy điểm D sao cho AB = AD

a) Chứng minh tam giác ACB = tam giác ACD từ đó suy ra tam giác BCD cân.

b) Gọi E, F lần lượt là trung điểm của CD và BC, BE cắt CA tại I. Chứng minh, D, I, F thẳng hàng.

c) Kẻ đường thẳng qua D, song song BC và cắt BE tại M. Gọi G là giao điểm của MA và CD. Chứng minh BC = 6GF

Giúp tui câu này nha 🥺

Với n = 1 > 0, ta có:

2ⁿ + 2 = 4

2n + 5 = 7

Mà 4 < 7

⇒ 2ⁿ + 2 > 2n + 5 là vô lí

Em xem lại đề nhé

2ⁿ⁺² mà chị có phải 2ⁿ+2 đâu ạ

g: \(\left(3x^4-2x^3+x^2\right):\dfrac{1}{3}x^2\)

\(=\dfrac{3x^4}{\dfrac{1}{3}x^2}-\dfrac{2x^3}{\dfrac{1}{3}x^2}+\dfrac{x^2}{\dfrac{1}{3}x^2}\)

\(=9x^2-6x+3\)

h: \(\dfrac{x^3-3x^2+6x}{-3x}\)

\(=-\dfrac{x^3}{3x}+\dfrac{3x^2}{3x}-\dfrac{6x}{3x}\)

\(=-\dfrac{1}{3}x^2+x-2\)

i: \(\dfrac{2x^2-5x+3}{2x-3}\)

\(=\dfrac{2x^2-3x-2x+3}{2x-3}\)

\(=\dfrac{x\left(2x-3\right)-\left(2x-3\right)}{2x-3}=x-1\)

j: \(\dfrac{x^5+x+1}{x^3-x}\)

\(=\dfrac{x^5-x^3+x^3-x+2x+1}{x^3-x}\)

\(=\dfrac{x^2\left(x^3-x\right)+\left(x^3-x\right)+2x+1}{x^3-x}\)

\(=x^2+1+\dfrac{2x+1}{x^3-x}\)

làm giùm mình câu g h i j mình cần gấp

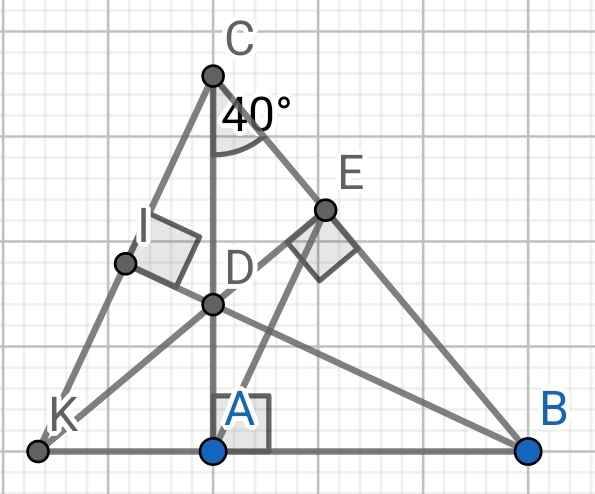
a) ∆ABC vuông tại A (gt)

⇒ ∠CBA + ∠ACB = 90⁰

⇒ ∠CBA = 90⁰ - ∠ACB

= 90⁰ - 40⁰

= 50⁰

b) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét hai tam giác vuông: ∆ABD và ∆EBD có:

BD là cạnh chung

∠ABD = ∠EBD (cmt)

⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)

c) Do ∆ABD = ∆EBD (cmt)

⇒ AD = ED (hai cạnh tương ứng)

⇒ ∆ADE cân tại D

d) Do CI ⊥ BD (gt)

⇒ BI ⊥ CK

⇒ BI là đường cao của ∆BCK

Do ∆ABC vuông tại A (gt)

⇒ CA ⊥ AB 

⇒ CA ⊥ BK

⇒ CA là đường cao thứ hai của ∆BCK

Mà CA và BI cắt nhau tại D

⇒ KD là đường cao thứ ba của ∆BCK

Mà DE ⊥ BC (gt)

⇒ K, D, E thẳng hàng

a) (2x³ - 3x² + x) + (x³ - x² + 2x + 1)

= 2x³ - 3x² + x + x³ - x² + 2x + 1

= (2x³ + x³) + (-3x² - x²) + (x + 2x) + 1

= 3x³ - 4x² + 3x + 1

b) (2x³ - 3x² + x) - (x³ - x² + 2x + 1)

= 2x³ - 3x² + x - x³ + x² - 2x - 1

= (2x³ - x³) + (-3x² + x²) + (x - 2x) - 1

= x³ - 2x² - x - 1

e) (2x + 1)(x³ - 4x + 5)

= 2x.(x³ - 4x + 5) + 1.(x³ - 4x + 5)

= 2x⁴ - 8x² + 10x + x³ - 4x + 5

= 2x⁴ + x³ - 8x² + (10x - 4x) + 5

= 2x⁴ + x³ - 8x² + 6x + 5

f) 3(x² - 2x)(3x + 1)

= (3x² - 6x)(3x + 1)

= 3x²(3x + 1) - 6x(3x + 1)

= 3x².3x + 3x².1 - 6x.3x - 6x.1

= 9x³ + 3x² - 18x² - 6x

= 9x³ + (3x² - 18x²) - 6x

= 9x³ - 15x² - 6x

là 1.25 nhé

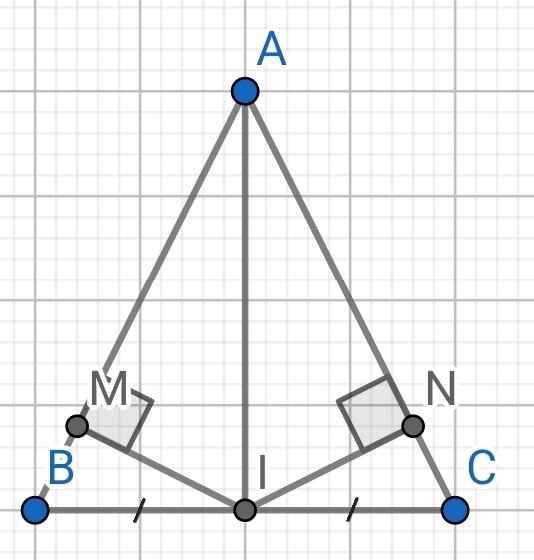
a) Do I là trung điểm của BC (gt)

⇒ BI = CI

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆AIB và ∆AIC có:

AB = AC (cmt)

AI là cạnh chung

BI = CI (cmt)

⇒ ∆AIB = ∆AIC (c-c-c)

b) Do AB = AC (cmt)

⇒ A nằm trên đường trung trực của BC (1)

Do BI = CI (cmt)

⇒ I nằm trên đường trung trực của BC (2)

Từ (1) và (2) ⇒ AI là đường trung trực của BC

⇒ AI ⊥ BC

c) ∆ABC cân tại A (gt)

AI là đường trung trực của BC

⇒ AI là đường phân giác của ∆ABC

⇒ ∠BAI = ∠CAI

⇒ ∠MAI = ∠NAI

Xét hai tam giác vuông: ∆AIM và ∆AIN có:

AI là cạnh chung

∠MAI = ∠NAI (cmt)

⇒ ∆AIM = ∆AIN (cạnh huyền - góc nhọn)

⇒ IM = IN (hai cạnh tương ứng)

⇒ ∆IMN cân tại I