a: Để A là số nguyên thì \(n-5⋮n+1\)

=>\(n+1-6⋮n+1\)

=>\(-6⋮n+1\)

=>\(n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

=>\(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)

Khi n=0 thì \(A=\dfrac{0-5}{0+1}=-5< 0\)(nhận)

Khi n=-2 thì \(A=\dfrac{-2-5}{-2+1}=\dfrac{-7}{-1}=7>0\left(loại\right)\)

Khi n=1 thì \(A=\dfrac{1-5}{1+1}=\dfrac{-4}{2}=-2< 0\)(nhận)

Khi n=-3 thì \(A=\dfrac{-3-5}{-3+1}=\dfrac{-8}{-2}=4>0\)(loại)

Khi n=2 thì \(A=\dfrac{2-5}{2+1}=\dfrac{-3}{3}=-1< 0\)(nhận)

Khi n=-4 thì \(A=\dfrac{-4-5}{-4+1}=\dfrac{-9}{-3}=3>0\left(loại\right)\)

Khi n=5 thì \(A=\dfrac{5-5}{5+1}=0\left(loại\right)\)

Khi n=-7 thì \(A=\dfrac{-7-5}{-7+1}=\dfrac{-12}{-6}=2>0\left(loại\right)\)

b: \(A=\dfrac{n-5}{n+1}=\dfrac{n+1-6}{n+1}=1-\dfrac{6}{n+1}\)

Để A có giá trị nhỏ nhất thì \(-\dfrac{6}{n+1}\) nhỏ nhất

=>\(\dfrac{6}{n+1}\) lớn nhất

=>n+1=1

=>n=0

Để A có giá trị lớn nhất thì \(\dfrac{6}{n+1}\) nhỏ nhất

=>n+1=-1

=>n=-2

136 nghìn đồng =100 000đ+30 000đ+6 000đ nên 

số tiền 100 000đ cần trả là:100 000:100 000=1(tờ)

số tiền 10 000đ cần trả là:30 000:10 000=3(tờ)

số tiền 1 000đ cần trả là:6 000:1 000=6(tờ)

Vậy cần trả 1 tờ 100 000đ,3 tờ 10 000đ,6 tờ 1 000đ

TICK CHO MIK VỚI NHÉ

Tú trả bác bán hàng như sau:

+ 1 tờ 100.000 đồng

+ 3 tờ 10.000 đồng

+ 6 tờ 1.000 đồng

Tổng: 1 x 100.000 + 3 x 10.000 + 6 x 1.000 = 136.000

Thỏa mãn đề bài 136.000 và mỗi loại không quá 9 tờ

TA CÓ:a:5 dư 3 suy ra:a+2 chia hết cho 5

                          suy ra a+17 chia hết cho 5    (1)

           a:7 dư 4 suy ra a+3 chia hết cho 7

                         suy ra a+17 chia hết cho 7      (2)

Từ (1) và (2) suy ra a+17 thuộc BC của 7 và 5

mà a nhỏ nhất nên a+17 thuộc BCNN của 7 và 5=35

suy ra a=35-17=18

Vậy a=18

TICK CHO MIK VỚI NHÉ

18

Đổi: 2 giờ 30 phút = 150 phút và 2 giờ 20 phút = 140 phút

Tỉ số thời gian máy bay thứ nhất so với máy bay thứ hai là: \(\dfrac{150}{140}=\dfrac{15}{14}\)

Cùng một quãng đường AB, thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch

Do đó nên tỉ số vận tốc máy bay thứ nhất so với máy bay thứ hai là: \(\dfrac{14}{15}\)

Coi vận tốc máy bay thứ nhất có giá trị 14 phần, vận tốc máy bay thứ hai có giá trị 15 phần

Hiệu số phần bằng nhau: 15-14=1 (phần)

Vận tốc máy bay thứ nhất: 1:1x14=14 (km/p) = 840 (km/giờ)

Vận tốc máy bay thứ hai: 14+1=15(km/p)=900(km/giờ)

Một phút máy bay thứ nhất bay chậm hơn máy bay thứ hai 1km tức một giờ máy bay thứ nhất chậm hơn máy bay thứ hai 60 km . Nói cách khác là vận tốc của hai máy bay có hiệu là 60km/h 

Thời gian máy bay thứ nhất bay là : 2 giờ 30 phút = 5/2​giờ 

Thời gian máy bay thứ hai bay là : 2 giờ 20 phút = 7/3​giờ 

Do cùng quãng đường bay nên tỉ số vận tốc hai máy bay tỉ lệ nghịch với tỉ số thời gian .

Ta có tỉ lệ :

Vận tốc máy bay thứ nhất/Vận tốc máy bay thứ hai = Thời gian máy bay hai bay/thời gian máy bay nhất bay

= 7/3:5/2​= 14/15

Vẽ sơ đồ hiệu số phần bằng nhau là : 15 - 14 = 1 (phần)

Hiệu hai vận tốc là 60km/giờ.

Vậy máy bay thứ nhất bay :

         60:1𝑥14=840( km/h )

Máy bay thứ hai bay là :

         60:1𝑥15=900( km/h )

Cách 1:

Gọi số phải tìm là: \(\overline{ab}\) (\(a\inℕ^∗;b\inℕ;a,b\le9\))

Theo bài ra, ta có:

\(b\times8=\overline{ab}\\ b\times8=\overline{a0}+b\\ b\times8-b=a\times10\\ b\times7=a\times10\\ b\times7:10=a\\ b\times0,7=a\)

Thử lần lượt b từ 0 đến 9, nếu giá trị nào cho a là STN khác 0 và a bé hơn hoặc bằng 9 thì nhận 

Kết quả: Không có giá trị nào thỏa mãn. Vậy không tìm được số thỏa mãn đề bài

Cách 2: Tương tự đến \(b\times7=\overline{a0}\)

Nhận thấy các số từ 0 đến 9 không có số nào nhân với 7 ra được số có tận cùng là 0

( Số 0 bị loại do 0 x 7 = 0 không phải số có 2 chữ số )

Ta có:

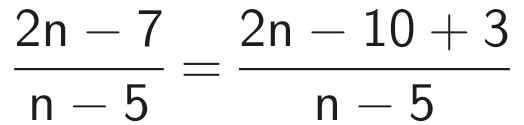
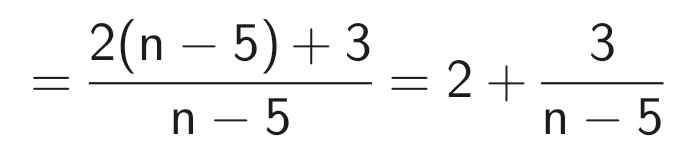
Để M nguyên thì 3 ⋮ (n - 5)

⇒ n - 5 ∈ Ư(3) = {-3; -1; 1; 3}

⇒ n ∈ {2; 4; 6; 8}

Vậy n {2; 4; 6; 8} thì M nguyên

TH1

𝑥≥0x≥0

=> |x-3| = x - 3 = 2x + 4

=> x - 2x = 4 + 3

=> -x = 7 <=> x = -7

x < 0

=> |x-3| = -x + 3 = 2x + 4

=> -x - 2x = 4-3

=> -3x = 1

=> x= -1/3

\(\overline{abcabc}=\overline{abc000}+\overline{abc}\\ =\overline{abc}\times1000+\overline{abc}\times1\\ =\overline{abc}\times1001=\overline{abc}\times7\times13\times11⋮7,13,11\)

Do 7, 13, 11 là 3 số nguyên tố hay STN có dạng trên chia hết cho ít nhất 3 SNT (DPCM)

Thời gian đi bộ của người đó:

   5 giờ 30 phút - 5 giờ = 30 (phút) = 1/2 (giờ)

Thời gian đi ô tô của người đó:

   7 giờ 50 phút - 5 giờ 30 phút = 2 giờ 20 phút = 7/3 giờ

Quãng đường đi bộ người đó đi được:

  \(6\times\dfrac{1}{2}=3\left(km\right)\)

Quãng đường đi ô tô đi được:

  \(54\times\dfrac{7}{3}=126\left(km\right)\)

Quãng đường người đó đã đi được:

  \(3+126=129\left(km\right)\)

    Đ/S:129km

\(-25-(x+2):3=-(-21)-47\\\Rightarrow -25-(x+2):3=21-47\\\Rightarrow -25-(x+2):3=-26\\\Rightarrow (x+2):3=-25-(-26)\\\Rightarrow (x+2):3=1\\\Rightarrow x+2=3\\\Rightarrow x=3-2\\\Rightarrow x=1\)

a: \(-25-\left(x+2\right):3=-\left(-21\right)-47\)

=>\(-25-\dfrac{x+2}{3}=21-47=-26\)

=>\(\dfrac{x+2}{3}+25=26\)

=>\(\dfrac{x+2}{3}=1\)

=>x+2=3

=>x=1