Tính : 109 - 1 ⋮ 999
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Olm chào em, đây là dạng toán nâng cao chuyên đề tìm giá trị của nhiều phần biết giá trị một số phần như thế, cấu trúc thi chuyên thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dãn các em giải chi tiết dạng này bằng phương pháp rút về đơn vị.
Giải:
77 cây hơn 56 cây số cây là:
77 - 56 = 21 (cây)
21 cây ứng với số cây của 3 công nhân trồng được trong một ngày.
Từ lập luận trên ta có số cây mỗi công nhân trồng được trong một ngày là:
21 : 3 = 7 (cây)
Sau khi thêm 3 người đội công nhân đó có số người là:
77 : 7 = 11 (người)
Ban đầu đội công nhân đó có số người là:
11 - 3 = 8 (người)
Đáp số: 8 người.
Lời giải:
3 công nhân trồng được số cây là: 77 - 56 = 21 (Cây)
Số cây 1 người trồng được là: 21:3 = 7 (Cây)
Vậy số công nhân trong đội trồng cây là: 56 : 7 = 8 (Công nhân)
Đáp số: 8 (Công nhân)

Tổ 3 người trong 1 ngày đóng được số bộ bàn ghế là:
\(75:5=15\) (bộ)
Tổ 5 người trong 1 ngày đóng được số bộ bàn ghế là:
\(15\times5:3=25\) (bộ)
Tổ 5 người trong 7 ngày đóng được số bộ bàn ghế là:
\(25\times7=175\) (bộ)

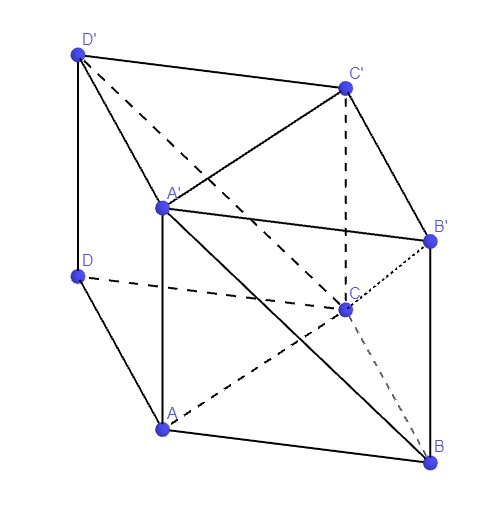
Gọi độ dài cạnh lăng trụ là a
Trong mp (ABC), lấy D đối xứng B qua AC \(\Rightarrow ABCD\) là hình thoi
Trong mp (A'B'C') lấy D' đối xứng B' qua A'C' \(\Rightarrow A'B'C'D'\) là hình thoi
\(\Rightarrow A'BCD'\) là hình bình hành nên \(A'B||D'C\)
\(\Rightarrow\left(A'B,B'C\right)=\left(D'C,B'C\right)=\widehat{B'CD'}\) (nếu nó nhọn, và bằng góc bù với nó nếu nó tù)
\(D'C=A'B=\sqrt{A'A^2+AB^2}=a\sqrt{2}\)
\(B'C=\sqrt{B'B^2+BC^2}=a\sqrt{2}\)
\(B'D'=BD=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Áp dụng định lý hàm cos:
\(cos\widehat{B'CD'}=\dfrac{B'C^2+D'C^2-B'D'^2}{2B'C.D'C}=\dfrac{1}{4}\)
\(\Rightarrow\left(A'B,B'C\right)\approx75^031'\)

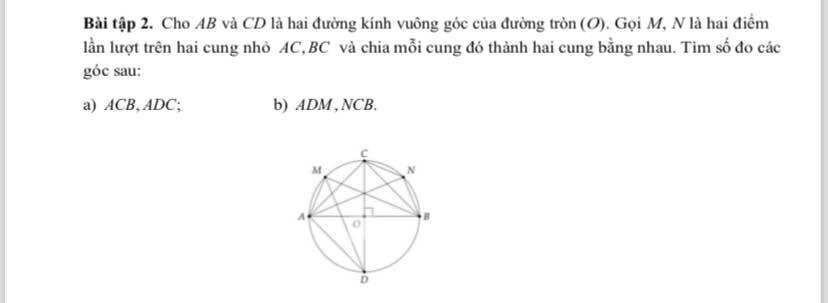
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>\(\widehat{ACB}=90^0\)
Xét (O) có \(\widehat{ADC}\) là góc nội tiếp chắn cung AC
nên \(\widehat{ADC}=\dfrac{\widehat{AOC}}{2}=\dfrac{90^0}{2}=45^0\)
b: M là điểm chia cung AC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{MA}=\dfrac{sđ\stackrel\frown{AC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét (O) có \(\widehat{ADM}\) là góc nội tiếp chắn cung AM
nên \(\widehat{ADM}=\dfrac{1}{2}\cdot sđ\stackrel\frown{MA}=\dfrac{1}{2}\cdot45^0=22,5^0\)
N chia cung BC thành hai cung nhỏ bằng nhau
=>\(sđ\stackrel\frown{BN}=\dfrac{sđ\stackrel\frown{BC}}{2}=45^0\)
Xét (O) có
\(\widehat{NCB}\) là góc nội tiếp chắn cung NB
=>\(\widehat{NCB}=\dfrac{sđ\stackrel\frown{NB}}{2}=\dfrac{45^0}{2}=22,5^0\)

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC
b: Xét (O) có
ΔCBD nội tiếp
CD là đường kính
Do đó: ΔCBD vuông tại B
=>CB\(\perp\)BD
mà AO\(\perp\)BC
nên AO//BD

Tuổi hiện nay của ông là:
(78+60):2=138:2=69(tuổi)
Tuổi cháu hiện nay là 69-60=9(tuổi)

a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
=>\(\widehat{yOz}=100^0-30^0=70^0\)
Vì tia Ot nằm trong góc yOz
nên tia Ot nằm giữa hai tia Oy,Oz
=>\(\widehat{yOt}+\widehat{zOt}=\widehat{yOz}\)
=>\(\widehat{zOt}=70^0-20^0=50^0\)
Vì \(\widehat{yOt}< \widehat{zOt}\left(20^0< 50^0\right)\)
nên Ot không là phân giác của góc yOz
b: Vì \(\widehat{zOt}< \widehat{zOx}\left(50^0< 100^0\right)\)
nên tia Ot nằm giữa hai tia Oz và Ox
=>\(\widehat{tOz}+\widehat{tOx}=\widehat{xOz}\)
=>\(\widehat{xOt}=100^0-50^0=50^0\)
Ta có: tia Ot nằm giữa hai tia Ox và Oz
mà \(\widehat{xOt}=\widehat{zOt}\left(=50^0\right)\)
nên Ot là phân giác của góc xOz

Em xem lại đề nhé
Ta có:
`10^9 - 1`
`= (10^3)^3 - 1^3`
`= 1000^3 - 1^3`
`= (1000 - 1)(1000^2 + 1000 . 1 + 1^2)`
`= 999 . (1000^2 + 1000 + 1) \vdots999 (đpcm)`
Vậy: `10^9 - 1 \vdots 999`