giúp em với các anh chị ơi 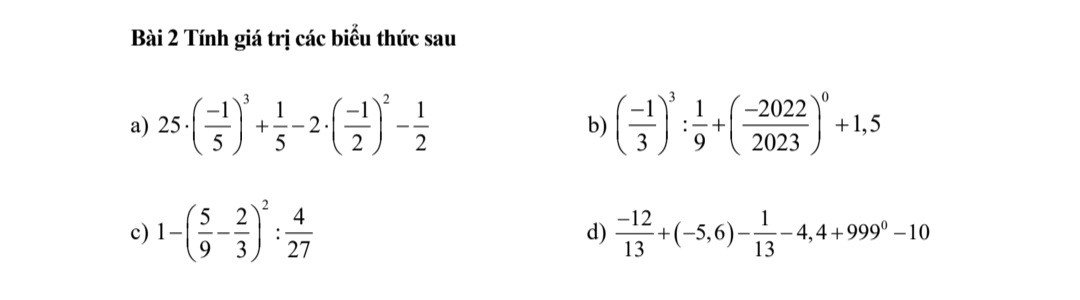
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 7:
$\frac{x}{6}-\frac{2}{y}=\frac{1}{30}$
$\frac{xy-12}{6y}=\frac{1}{30}$
$\frac{5(xy-12)}{30y}=\frac{y}{30y}$
$\Rightarrow 5(xy-12)=y$
$\Rightarrow 5xy-60-y=0$
$\Rightarrow y(5x-1)=60$
Do $x,y$ là số nguyên nên $5x-1$ cũng là số nguyên. Mà $y(5x-1)=60$ nên $5x-1$ là ước của $60$.
Mà $5x-1$ chia $5$ dư $4$ nên:
$5x-1\in \left\{-1; -6;4\right\}$
Với $5x-1=-1\Rightarrow x=0$
$y=\frac{60}{5x-1}=\frac{60}{-1}=-60$
Với $5x-1=-6\Rightarrow x=-1$
$y=\frac{60}{-6}=-10$
Với $5x-1=4\Rightarrow x=1$
$y=\frac{60}{4}=15$
Vậy $(x,y)=(0,-60), (-1,-10), (1,15)$
Bài 6:
a. $(x+1)+(x+2)+(x+3)+...+(x+100)=5750$
$(x+x+....+x)+(1+2+3+...+100)=5750$
Số lần xuất hiện của $x$: $(100-1):1+1=100$
Do đó:
$100x+(1+2+3+...+100)=5750$
$100x+100.101:2=5750$
$100x+5050=5750$
$100x=700$
$x=700:100$
$x=7$
b.
\((\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{8.9.10})x=\frac{44}{45}\\ (\frac{2}{1.2.3}+\frac{2}{2.3.4}+...+\frac{2}{8.9.10})x=\frac{88}{45}\\ (\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+...+\frac{10-8}{8.9.10})x=\frac{88}{45}\\ (\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{8.9}-\frac{1}{9.10})x=\frac{88}{45}\\ (\frac{1}{1.2}-\frac{1}{9.10})x=\frac{88}{45}\\ \frac{22}{45}x=\frac{88}{45}\\ x=\frac{88}{45}: \frac{22}{45}=4\)

A)(Cái này mk ko biết tính nhanh)
= 252 + 57
= 309
B)= (238 x 5) x (25 x 34)
= 1190 x 850
= 1 011 500
A; 398 - 146 + 111 - 54
= (398 + 111) - (146 + 54)
= 509 - 200
= 309
B, 238 x 34 x 25 x 5
= 119 x 2 x 2 x 17 x 25 x 5
= (119 x 5 x 17) x (2 x 2 x 25)
= (595 x 17) x (4 x 25)
= 10115 x 100
= 1011500



Bài 1:
$C=3+8+13+\dots+123+128$
Số các số hạng của C là:
$(128-3):5+1=26$ (số)
Tổng C bằng:
$(128+3)\cdot26:2=1703$
$---$
$D=2+9+16+\dots+142+149$
Số các số hạng của D là:
$(149-2):7+1=22$ (số)
Tổng D bằng:
$(149+2)\cdot22:2=1661$
Bài 2:
a) Số hạng thứ 60 của tổng đó là:
$(60-1)\cdot6+4=358$
b) Tổng của 60 số hạng đầu tiên trong tổng S là:
$(358+4)\cdot60:2=10860$

a) \(A=1+4+7+...+124\)
Số lượng số hạng: (124 - 1) : 3 + 1 = 42 (số hạng)
\(A=\dfrac{\left(124+1\right)\cdot42}{2}=2625\)
b) \(B=2+6+10+...+122+126\)
Số lượng số hạng: \(\left(126-2\right):4+1=32\) (số hạng)
\(B=\dfrac{\left(126+2\right)\cdot32}{2}=2048\)

$-\frac38\times\frac16+\frac{3}{-8}\times\frac56+\frac{-10}{16}$
$=-\frac38\times(\frac16+\frac56)-\frac58$
$=-\frac38\times1-\frac58$
$=-\frac38-\frac58=-\frac88=-1$
\(\dfrac{-3}{8}\cdot\dfrac{1}{6}+\dfrac{3}{-8}\cdot\dfrac{5}{6}+\dfrac{-10}{16}\\ =\dfrac{-3}{8}\cdot\dfrac{1}{6}+\dfrac{-3}{8}\cdot\dfrac{5}{6}+\dfrac{-5}{8}\\ =\dfrac{-3}{8}\cdot\left(\dfrac{1}{6}+\dfrac{5}{6}\right)+\dfrac{-5}{8}\\ =-\dfrac{3}{8}\cdot1+\dfrac{-5}{8}\\ =\dfrac{-3-5}{8}\\ =-1\)

a)
\(25\cdot\left(\dfrac{-1}{5}\right)^3+\dfrac{1}{5}-2\left(\dfrac{-1}{2}\right)^2-\dfrac{1}{2}\\=-\dfrac{1}{5}\cdot\left[25\cdot\left(-\dfrac{1}{5}\right)^2+1\right]-\dfrac{1}{2}\left[2\cdot\left(-\dfrac{1}{2}\right)+1\right]\\ =-\dfrac{1}{5}\cdot\left(25\cdot\dfrac{1}{25}+1\right)-\dfrac{1}{2}\left(-1+1\right)\\ =-\dfrac{1}{5}\left(1+1\right)-\dfrac{1}{2}\cdot0\\ =-\dfrac{1}{5}\cdot2\\ =-\dfrac{2}{5}\)
b)
\(\left(-\dfrac{1}{3}\right)^3:\dfrac{1}{9}+\left(\dfrac{-2022}{2023}\right)^0+1,5\\ =\left(-\dfrac{1}{3}\right)^3:\left(-\dfrac{1}{3}\right)^2+1+1,5\\ =\left(-\dfrac{1}{3}\right)+1+\dfrac{3}{2}\\ =\dfrac{-2}{6}+\dfrac{6}{6}+\dfrac{9}{6}\\ =\dfrac{13}{6}\)
c)
\(1-\left(\dfrac{5}{9}-\dfrac{2}{3}\right):\dfrac{4}{27}\\ =1-\left(\dfrac{5}{9}-\dfrac{6}{9}\right):\dfrac{4}{27}\\ =1-\dfrac{-1}{9}:\dfrac{4}{27}\\ =1+\dfrac{1}{9}\cdot\dfrac{27}{4}\\ =1+\dfrac{3}{4}\\ =\dfrac{7}{4}\)
d)
\(\dfrac{-12}{13}+\left(-5,6\right)-\dfrac{1}{13}-4,4+999^0-10\\ =\dfrac{-12}{13}+\dfrac{-28}{5}-\dfrac{1}{13}-\dfrac{22}{5}+1-10\\ =\left(\dfrac{-12}{13}-\dfrac{1}{13}\right)+\left(\dfrac{-28}{5}-\dfrac{22}{5}\right)+\left(1-10\right)\\ =\dfrac{-13}{13}+\dfrac{-50}{5}+\left(-9\right)\\ =\left(-1\right)+\left(-10\right)+\left(-9\right)\\ =-20\)
a)