- Cách 1: $A=\{17;18;19;20;21;22;23\}$

- Cách 2: $A=\{x\in \mathbb{N}^*|17< x\le 23\}$

tk

c1 :A ={ 18 ;19;20;21;22;23;24}

c2 : A = { x E N / 17<x<25}

(-15)x2-240-6+36:(-6)x2

=-30-246+(-6)x2

=-276-12=-288

\(\left(-15\right)\times2-240-6+36:\left(-6\right)\times2\)

\(=-\left(15\times2\right)-240-6+\left[-\left(36:6\right)\times2\right]\)

\(=\left(-30\right)-240-6+\left[-6\times2\right]\)

\(=\left(-30\right)-240-6+\left(-12\right)\)

\(=-270-6+\left(-12\right)\)

\(=-276+\left(-12\right)\)

\(=-288\)

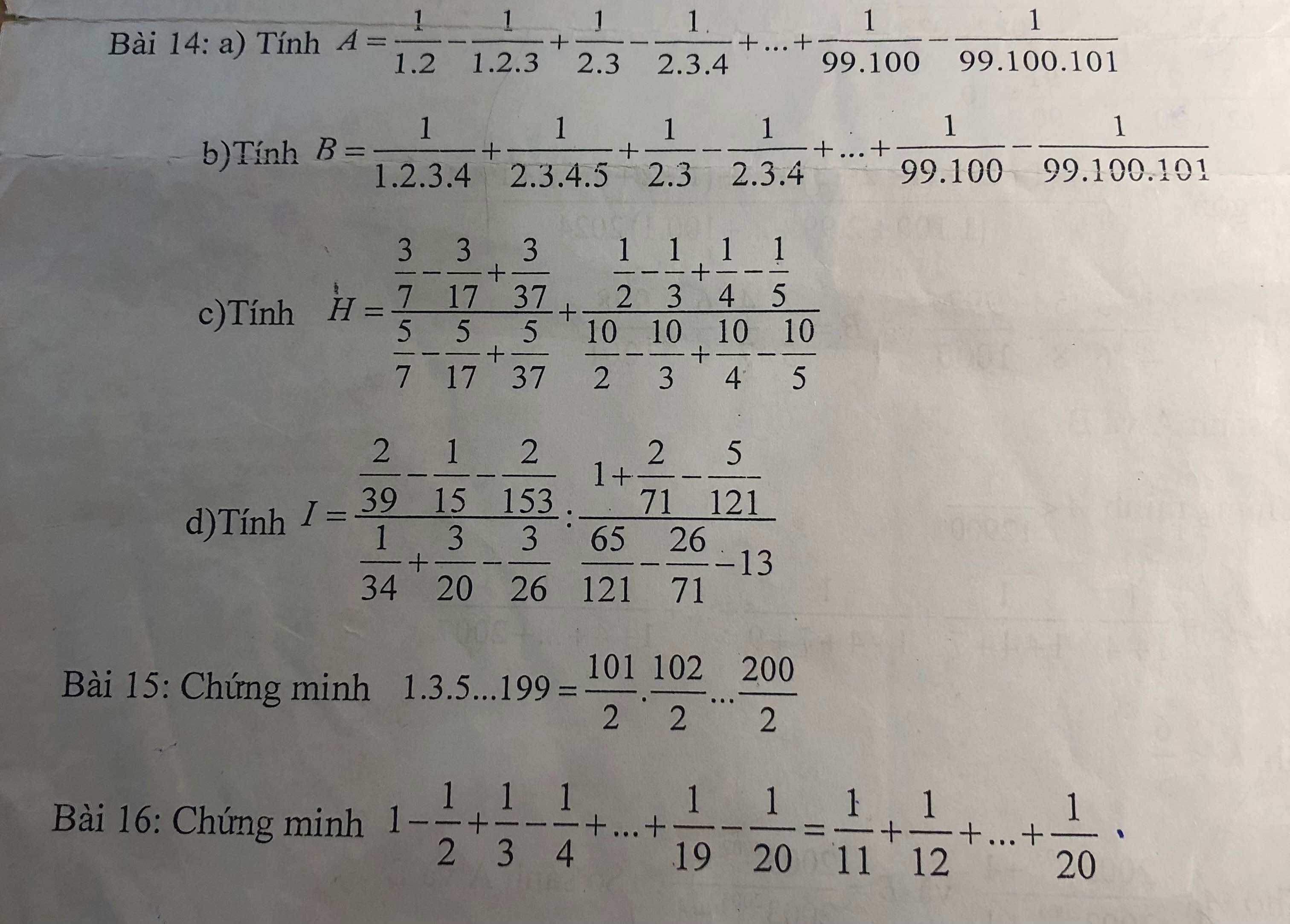
Bài 14:

c) 

\(H=\dfrac{\dfrac{3}{7}-\dfrac{3}{17}+\dfrac{3}{37}}{\dfrac{5}{7}-\dfrac{5}{17}+\dfrac{5}{37}}+\dfrac{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}}{\dfrac{10}{2}-\dfrac{10}{3}+\dfrac{10}{4}-\dfrac{10}{5}}\\ =\dfrac{3\left(\dfrac{1}{7}-\dfrac{1}{17}+\dfrac{1}{37}\right)}{5\left(\dfrac{1}{7}-\dfrac{1}{17}+\dfrac{1}{37}\right)}+\dfrac{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}}{10\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}\right)}\\ =\dfrac{3}{5}+\dfrac{1}{10}\\ =\dfrac{6}{10}+\dfrac{1}{10}\\ =\dfrac{7}{10}\)

\(\left(-18-12\right):5\)

\(=-\left(18+12\right):5\)

\(=-30:5\)

\(=-6\)

   (- 18 - 12) : 5

= -(18 + 12) : 5

= - 30 : 5

=  - 6 

200x53+47x156+47x44

\(=200\cdot53+47\cdot\left(156+44\right)\)

\(=53\cdot200+47\cdot200=200\cdot\left(53+47\right)\)

\(=200\cdot100=20000\)

$200\times53+47\times156+47\times44$

$=47\times(156+44)+200\times53$

$=47\times200+200\times53$

$=200\times(47+53)$

$=200\times100=20000$

đố ai giải được

10000.159879.222 = 354931380000

giúp với

\(7\in A;11\notin A;0\in A;13\notin A\)

\(\dfrac{27\cdot45+27\cdot5}{2+4+6+...+14+16+18}\)

\(=\dfrac{27\left(45+5\right)}{\left(2+18\right)+\left(4+16\right)+\left(6+14\right)+\left(8+12\right)+10}\)

\(=\dfrac{27\cdot50}{20+20+20+20+10}=\dfrac{27\cdot50}{90}=27\cdot\dfrac{5}{9}=15\)

\(\dfrac{27\cdot45+27\cdot5}{2+4+6+...+18}\\ =\dfrac{27\cdot\left(45+5\right)}{\dfrac{\left[\left(18-2\right):2+1\right]\left(18+2\right)}{2}}\\ =\dfrac{27\cdot50}{\dfrac{\left(16:2+1\right)\cdot20}{2}}\\ =\dfrac{27\cdot50}{\left(8+1\right)\cdot10}\\ =\dfrac{27\cdot50}{9\cdot10}\\ =15\)

\(A=10^3+\left[20^2+\left(2^3\cdot3\cdot5-3^2\cdot5\right)\right]\\ =10^3+\left[20^2+\left(8\cdot3\cdot5-9\cdot5\right)\right]\\ =10^3+\left[20^2+\left(120-45\right)\right]\\ =1000+\left(400+75\right)\\ =1000+475\\ =1475\)

\(B=326+8\cdot\left[20^2+\left(65-5\cdot11\right)\right]\\ =326+8\cdot\left[20^2+\left(65-55\right)\right]\\ =326+8\cdot\left(400+10\right)\\ =326+8\cdot410\\ =326+3280\\ =3606\)

`#3107.101107`

`99 - 97 + 95 - 93 + ... + 3 - 1`

Số hạng của tổng trên:

`(99 - 1) \div 2 + 1 = 50`

Số cặp có trong tổng trên:

`50 \div 2 = 25` (cặp)

__

`99 - 97 + 95 - 93 + ... + 3 - 1`

`= (99 - 97) + (95 - 93) + ... + (3 - 1)`

`= 2 + 2 + ... + 2`

Tổng trên có `25` cặp `\rightarrow` Có `25` số `2` 

`= 2 \times 25 = 50.`

99 - 97 + 95 - 93 + ... + 3 - 1

= (99 - 97) + (95 - 93) + ... + (3 - 1)

số hạng có trong dãy số đó là:

(99 - 1) : 2 + 1 = 50

số cặp: 50 : 2 = 25 cặp số

tổng của dãy số là:

25 x (-2) = -50

vậy tổng của dãy số là -50