Bài 5. (0,5 điểm) Giải phương trình ẩn $x$: $\dfrac{x-a}{bc}+\dfrac{x-b}{ca}+\dfrac{x-c}{ab}=\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}$ với $a, \, b, \, c \in \mathbb{R}$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Với �=−1m=−1, hàm số trở thành �=−2�+1y=−2x+1.
Xét hàm số �=−2�+1y=−2x+1 :
Thay �=0x=0 thì �=1y=1.
Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (0;1)(0;1).
Thay �=1x=1 thì �=−1y=−1.
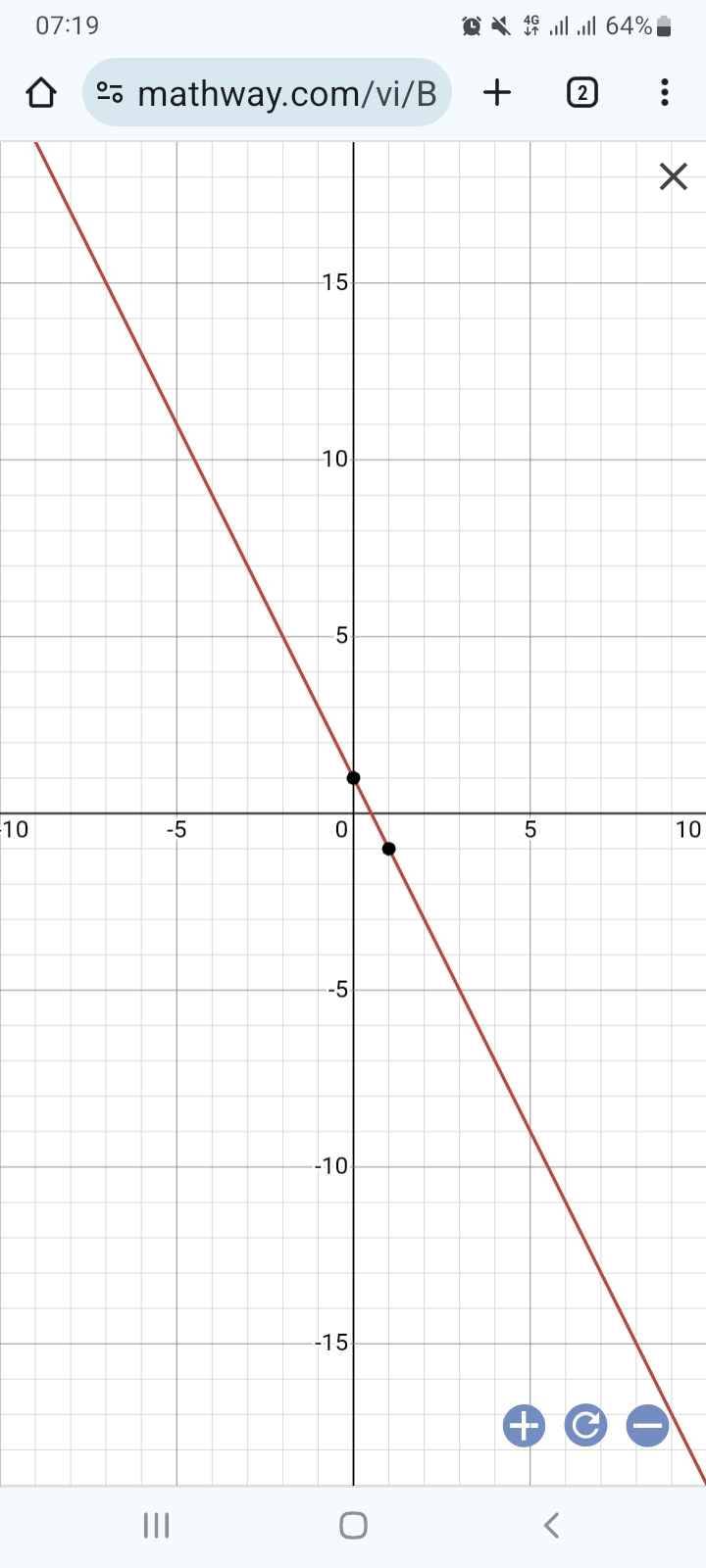
Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a=−3;b=9.
Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
khác 9.
Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b
Suy ra �=−5b=−5 (thoả mãn)
Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.
Suy ra đồ thị hàm số �=−2�+1y=−2x+1 đi qua điểm có tọa độ (1;−1)(1;−1).
Vẽ đồ thị:
Vì đường thẳng (�):�=��+�(d):y=ax+b song song với đường thẳng (�′ ):�=−3�+9(d′ ):y=−3x+9 nên: �≠−3;�≠9a
khác−3;b
khác 9.
Khi đó ta có: (�):�=−3�+�(d):y=−3x+b và �≠9b
khác 9.
Vì đường thẳng (�):�=��+�(d):y=ax+b đi qua �(1;−8)A(1;−8) nên: −8=−3.1+�−8=−3.1+b
Suy ra �=−5b=−5 (thoả mãn)
Vậy đường thẳng cần tìm là (�):�=−3�−5(d):y=−3x−5.

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)
20 phút = 1/3 h
Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)
Quãng đường đi từ thành phố về quê: 30x (km)
Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)
Theo đề bài, ta có phương trình:
30x = 25(x + 1/3)
30x = 25x + 25/3
30x - 25x = 25/3
5x = 25/3
x = 25/3 : 5
x = 5/3 (nhận)
Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) 3x - 5 = 4
3x = 4 + 5
3x = 9
x = 9 : 3
x = 3
Vậy S = {3}
b) 2x/3 + (3x - 1)/6 = x/2
4x + 3x - 1 = 3x
7x - 3x = 1
4x = 1
x = 1/4
Vậy S = {1/4}

a: Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=90^0\)
=>\(\widehat{IBC}+\widehat{ICB}=45^0\)
Xét ΔBIC có \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)
=>\(\widehat{BIC}+45^0=180^0\)
=>\(\widehat{BIC}=135^0\)

2a/
$(2x+1)^2(x-1)(x+2)=100$
$\Leftrightarrow (4x^2+4x+1)(x^2+x-2)=100$
Đặt $x^2+x=a$ thì PT trở thành:
$(4a+1)(a-2)=100$
$\Leftrightarrow 4a^2-8a+a-2=100$
$\Leftrightarrow 4a^2-7a-102=0$
$\Leftrightarrow (a-6)(4a+17)=0$
$\Leftrightarrow a-6=0$ hoặc $4a+17=0$
Nếu $a-6=0$
$\Leftrightarrow x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
Nếu $4a+17=0$
$\Leftrightarrow 4x^2+4x+17=0$
$\Leftrightarrow (2x+1)^2=-16<0$ (vô lý)
Vậy PT có nghiệm $x=2$ hoặc $x=-3$
2b/
\(\frac{b-c}{(a-b)(a-c)}+\frac{c-a}{(b-c)(b-a)}+\frac{a-b}{(c-a)(c-b)}=\frac{(a-c)-(a-b)}{(a-b)(a-c)}+\frac{(b-a)-(b-c)}{(b-c)(b-a)}+\frac{(c-b)-(c-a)}{(c-a)(c-b)}\\ =\frac{1}{a-b}-\frac{1}{a-c}+\frac{1}{b-c}-\frac{1}{b-a}+\frac{1}{c-a}-\frac{1}{c-b}\\ =\frac{1}{a-b}+\frac{1}{c-a}+\frac{1}{b-c}+\frac{1}{a-b}+\frac{1}{c-a}+\frac{1}{b-c}\\ =\frac{2}{a-b}+\frac{2}{b-c}+\frac{2}{c-a}\)
Ta có đpcm.

Gọi diện tích ruộng phải cày theo kế hoạch là x(ha)
(Điều kiện: x>0)
Thời gian dự kiến hoàn thành là \(\dfrac{x}{40}\left(ngày\right)\)
Diện tích ruộng thực tế cày được là x+4(ha)
Thời gian thực tế hoàn thành là \(\dfrac{x+4}{52}\left(ngày\right)\)
Đội đã hoàn thành trước 2 ngày nên ta có:
\(\dfrac{x}{40}-\dfrac{x+4}{52}=2\)
=>\(\dfrac{13x-10\left(x+4\right)}{520}=2\)
=>3x-40=1040
=>3x=1080
=>x=360(nhận)
Vậy: Diện tích ruộng phải cày theo kế hoạch là 360ha
Lời giải:
Giả sử theo dự định đội cần cày trong $a$ ngày.
Diện tích cày theo dự kiến: $40a$ (ha)
Diện tích cày thực tế: $52(a-2)$ (ha)
Theo bài ra ta có:
$40a+4=52(a-2)$
$\Leftrightarrow 12a=108$
$\Leftrightarrow a=9$ (ngày)
Diện tích ruộng phải cày theo kế hoạch:
$40a=40.9=360$ (ha)


Lời giải:
Giả sử ta xếp ngẫu nhiên 10 số tự nhiên đó với ký hiệu là $a_1,a_2,a_3,..., a_{10}$
Giả sử không tồn tại 3 số tự nhiên liền kề nhau có tổng lớn hơn hoặc bằng 17, tức là tổng 3 số liền kề bất kỳ luôn $\leq 16$
Khi đó:
$a_1+a_2+a_3\leq 16$
$a_2+a_3+a_4\leq 16$
$a_3+a_4+a_5\leq 16$
..............
$a_8+a_9+a_{10}\leq 16$
$a_9+a_{10}+a_1\leq 16$
$a_{10}+a_1+a_2\leq 16$
Cộng theo vế các BĐT trên lại và thu gọn:
$3(a_1+a_2+...+a_{10})\leq 16.10$
$\Leftrightarrow 3(1+2+3+...+10)\leq 160$
$\Leftrightarrow 165\leq 160$ (vô lý)
Do đó điều giả sử là sai. Tức là tồn tại ít nhất 3 số liền kề có tổng $\geq 17$.






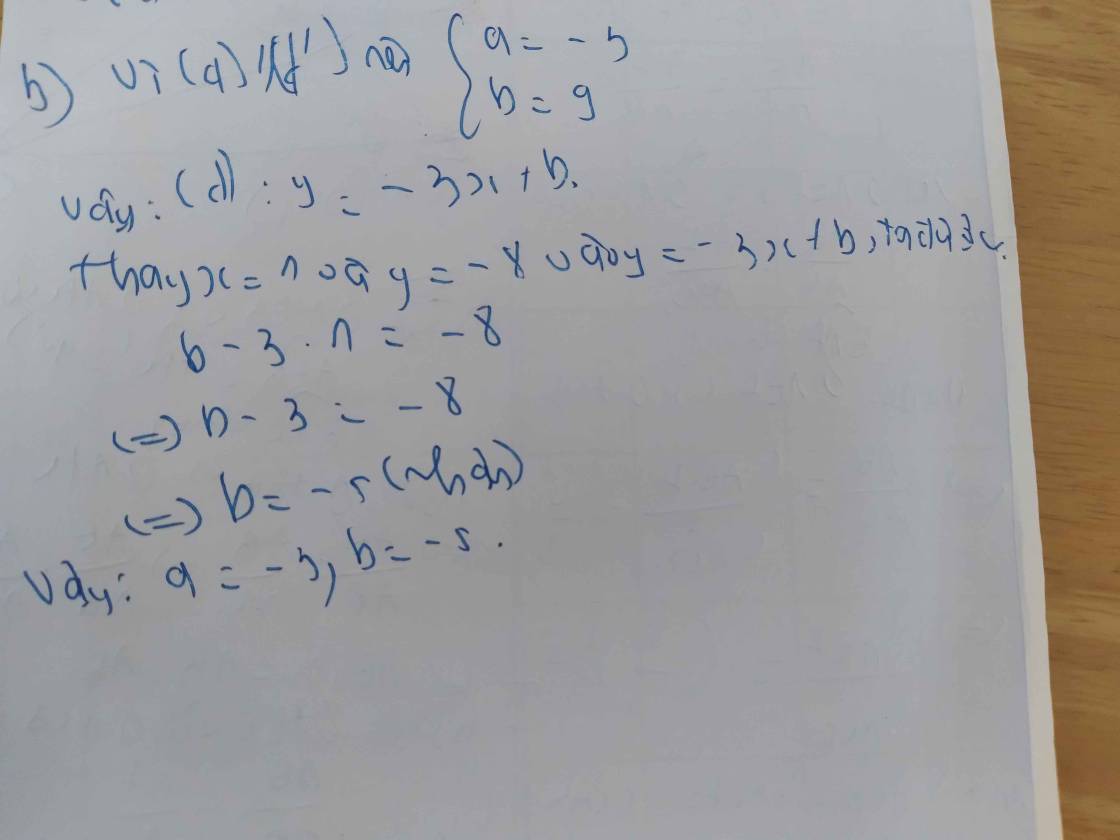

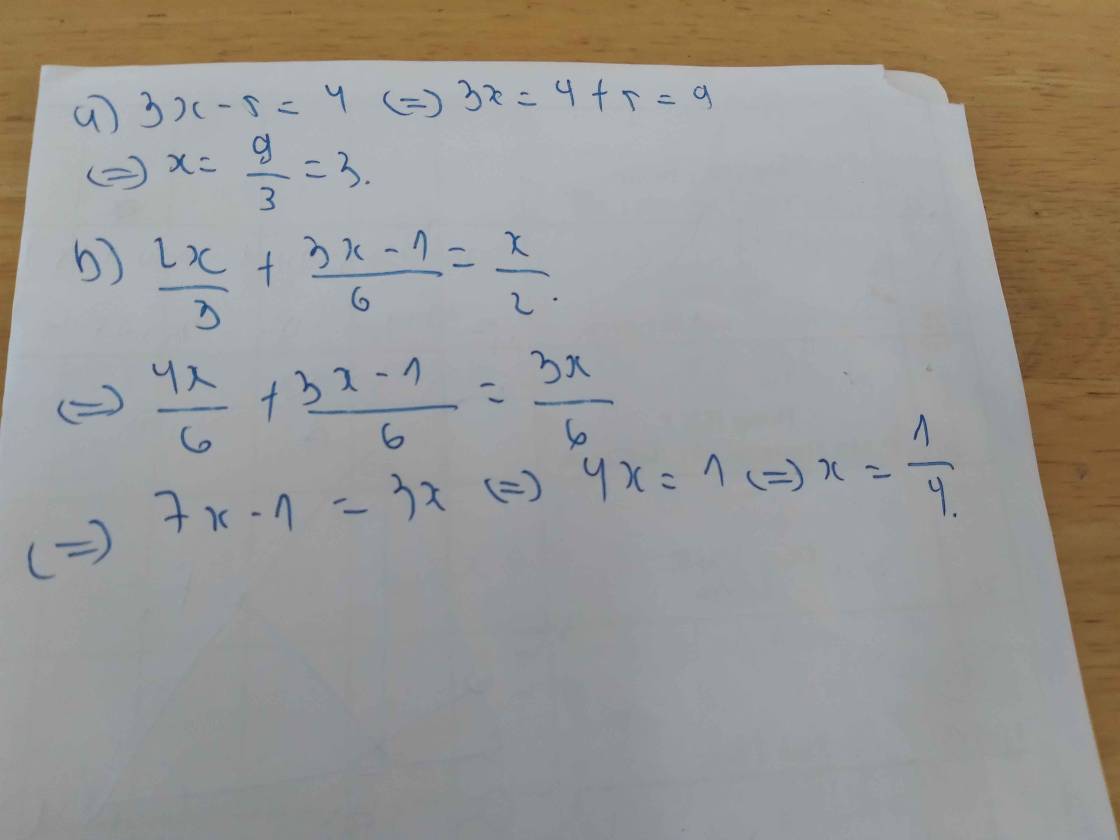

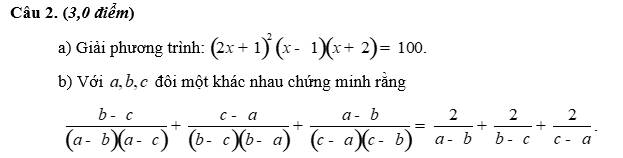
 ai giải
ai giải
(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c
a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab
ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab
(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab
(a + b + c)x = (a + b + c)²
x = (a + b + c)²/(a + b + c)
x = a + b + c
Vậy S = {a + b + c}
Ta có: 𝑥−𝑎𝑏𝑐+𝑥−𝑏𝑐𝑎+𝑥−𝑐𝑎𝑏=2𝑎+2𝑏+2𝑐bcx−a+cax−b+abx−c=a2+b2+c2
(𝑥−𝑎𝑏𝑐−2𝑎)+(𝑥−𝑏𝑐𝑎−2𝑏)+(𝑥−𝑐𝑎𝑏−2𝑐)=0(bcx−a−a2)+(cax−b−b2)+(abx−c−c2)=0
𝑎(𝑥−𝑎)−2𝑏𝑐+𝑏(𝑥−𝑏)−2𝑐𝑎+𝑐(𝑥−𝑐)−2𝑎𝑏𝑎𝑏𝑐=0abca(x−a)−2bc+b(x−b)−2ca+c(x−c)−2ab=0
Điều kiện xác định: 𝑎,𝑏,𝑐≠0a,b,c=0
Khi đó: (𝑎+𝑏+𝑐)𝑥−𝑎2−2𝑏𝑐−𝑏2−2𝑐𝑎−𝑐2−2𝑎𝑏𝑎𝑏𝑐=0abc(a+b+c)x−a2−2bc−b2−2ca−c2−2ab=0
(𝑎+𝑏+𝑐)𝑥=(𝑎+𝑏+𝑐)2(a+b+c)x=(a+b+c)2
+ Nếu 𝑎+𝑏+𝑐=0a+b+c=0 thì phương trình có vô số nghiệm.
+ Nếu 𝑎+𝑏+𝑐≠0a+b+c=0 thì phương trình có nghiệm duy nhất 𝑥=𝑎+𝑏+𝑐x=a+b+c.