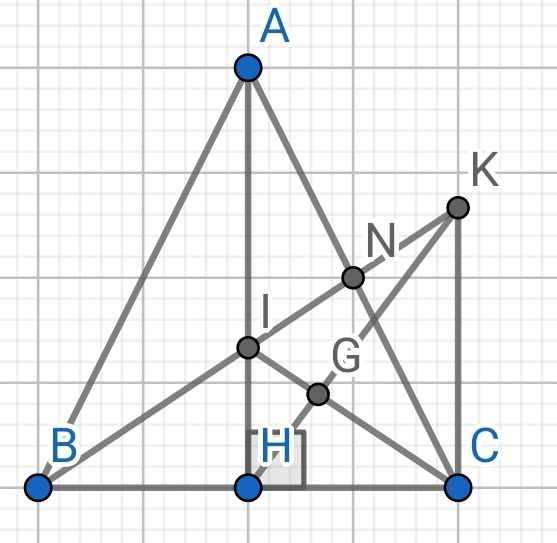
Tam giác ABC cân tại A . Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD=CE . Kẻ BH vuông góc với AD . Kẻ CK vuông góc với AE .chứng minh
a.BH=CK
b.tam giác ABH=tam giác ACK
c. gọi O là giao điểm của HB và KC . cm tam giác OBC cân
d.cm AO là phân giác của góc DAE
e. gọi I là trung điểm của BC . cm A,I ,O thẳng hàng

a: Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
=>AD=AE; \(\widehat{BAD}=\widehat{CAE};\widehat{ADB}=\widehat{AEC}\)
Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HDB}=\widehat{KEC}\)
Do đó: ΔHBD=ΔKCE
=>HB=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
Do đó: ΔAHB=ΔAKC
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)(hai góc đối đỉnh)
\(\widehat{OCB}=\widehat{KCE}\)(hai góc đối đỉnh)
mà \(\widehat{HBD}=\widehat{KCE}\)(ΔHBD=ΔKCE)
nên \(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
d: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{BAO}=\widehat{CAO}\)
Ta có: \(\widehat{DAB}+\widehat{BAO}=\widehat{DAO}\)
\(\widehat{EAC}+\widehat{CAO}=\widehat{EAO}\)
mà \(\widehat{DAB}=\widehat{EAC};\widehat{BAO}=\widehat{CAO}\)
nên \(\widehat{DAO}=\widehat{EAO}\)
=>AO là phân giác của góc DAE
e: IB=IC
=>I nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng