Cho tam giác ABC vuông tại a đường cao ah, ah=3 cm, sinb= 3/4. Tính ab, góc c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay m=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2x+y=3\cdot\left(-1\right)+1=-2\\3x+2y=2\cdot\left(-1\right)-3=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+2y=-4\\3x+2y=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+2y-3x-2y=-4+5\\2x+y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2-2x=-2-2=-4\end{matrix}\right.\)
b: Vì \(\dfrac{2}{3}\ne\dfrac{1}{2}\)
nên hệ luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}2x+y=3m+1\\3x+2y=2m-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+2y=6m+2\\3x+2y=2m-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+y=3m+1\\4x+2y-3x-2y=6m+2-2m+3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4m+5\\y=3m+1-2\left(4m+5\right)=3m+1-8m-10=-5m-9\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x< 1\\y< 6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m+5< 1\\-5m-9< 6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m< -4\\-5m< 15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -1\\m>-3\end{matrix}\right.\)
=>-3<m<-1

hpt \(\Leftrightarrow\left\{{}\begin{matrix}y=5-2x\\y+x^2=4x\end{matrix}\right.\)
\(\Rightarrow5-2x+x^2=4x\)
\(\Leftrightarrow x^2-6x+5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Nếu \(x=1\Rightarrow y=5-2x=3\)
Nếu \(x=5\Rightarrow y=5-2x=-5\)
Vậy hpt đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(1;3\right);\left(5;-5\right)\right\}\)

Bài 2:
Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
Bài 3:
a: Xét tứ giác MKHN có \(\widehat{MKN}=\widehat{MHN}=90^0\)
nên MKHN là tứ giác nội tiếp
b: Xét tứ giác PHIK có \(\widehat{PHI}+\widehat{PKI}=90^0+90^0=180^0\)
nên PHIK là tứ giác nội tiếp

Gọi vận tốc của ô tô thứ nhất là x(km/h)
(Điều kiện: x>0)
vận tốc của ô tô thứ hai là x+20(km/h)
Thời gian xe ô tô thứ nhất đi từ A đến chỗ gặp là:
10h30p-6h=4h30p=4,5(giờ)
Thời gian xe ô tô thứ hai đi từ A đến chỗ gặp là:
10h30p-7h30p=3(giờ)
Độ dài quãng đường ô tô thứ nhất đi từ A đến chỗ gặp là
4,5x(km)
Độ dài quãng đường ô tô thứ hai đi từ A đến chỗ gặp là:
3(x+20)(km)
Do đó, ta có phương trình:
4,5x=3(x+20)
=>4,5x=3x+60
=>1,5x=60
=>x=60:1,5=40(nhận)
Vậy: Vận tốc của ô tô thứ nhất là 40km/h
Vận tốc của ô tô thứ hai là 40+20=60km/h

Gọi x (phút) là thời gian làm việc một mình của thợ làm thứ nhất (x >0)
y (phút) là thời gian làm việc một mình của thợ làm thứ hai (y>0)
- Thợ làm thứ nhất hoàn thành công việc trong x giờ => 1 giờ thợ làm thứ nhất hoàn thành 1/x công việc. Tương tự, thợ làm thứ hai làm trong 1 giờ sẽ hoàn thành 1/y công việc.
Từ đó, ta có phương trình thứ nhất: 1/x + 1/y = 1/200 (1)
Người thứ nhất giảm năng suất đi 1,5 lần, tức trong 1 giờ người thứ nhất làm được 2/3x công việc, người thứ hai tăng năng suất lên 2,5 lần, tức người thứ hai làm được 5/2y công việc trong 1 giờ.
Từ đó, ta có phương trình thứ hai: 2/3x + 5/2y = 1/135 (2)
Bấm máy giải ra: x= 360 phút và y= 450 phút.
Vậy thợ làm thứ nhất làm một mình mất 360 phút, còn thợ làm thứ hai là 450 phút.

Kẻ đường kính MK của (O)
Xét (O) có
ΔMPK nội tiếp
MK là đường kính
Do đó: ΔMPK vuông tại P
Xét (O) có
\(\widehat{MNP}\) là góc nội tiếp chắn cung MP
\(\widehat{MKP}\) là góc nội tiếp chắn cung MP
Do đó: \(\widehat{MNP}=\widehat{MKP}\)
Ta có: \(\widehat{MNP}+\widehat{NMH}=90^0\)(ΔMHN vuông tại H)
\(\widehat{MKP}+\widehat{KMP}=90^0\)(ΔMKP vuông tại P)
mà \(\widehat{MNP}=\widehat{MKP}\)
nên \(\widehat{NMH}=\widehat{KMP}\)
=>\(\widehat{NMH}+\widehat{OMH}=\widehat{KMP}+\widehat{OMH}\)
=>\(\widehat{PMH}=\widehat{OMN}\)

Gọi lãi suất 1 năm của ngân hàng là x (%) (x>0)
Số tiền cả gốc lẫn lãi sau năm đầu tiên là:
\(20+20.\dfrac{x}{100}=20\left(1+\dfrac{x}{100}\right)\) (triệu)
Số tiền cả gốc lẫn lãi sau 2 năm là:
\(20\left(1+\dfrac{x}{100}\right)\left(1+\dfrac{x}{100}\right)=20\left(1+\dfrac{x}{100}\right)^2\) (triệu)
Do sau 2 năm chú nhận được 24 triệu nên ta có pt:
\(20\left(1+\dfrac{x}{100}\right)^2=24\)
\(\Leftrightarrow\left(1+\dfrac{x}{100}\right)^2=\dfrac{6}{5}\)
\(\Rightarrow1+\dfrac{x}{100}=\dfrac{\sqrt{30}}{5}\)
\(\Rightarrow x=20\sqrt{30}-100\approx9,54\left(\%\right)\)
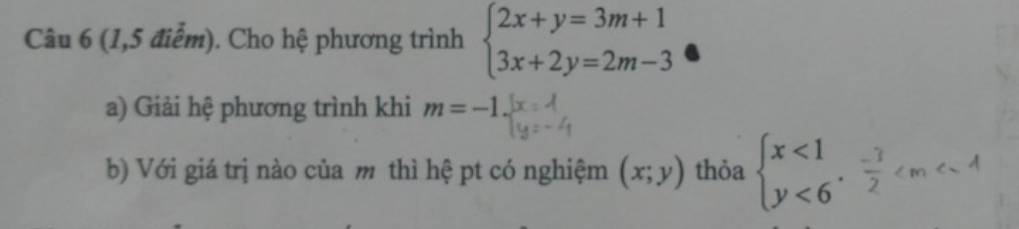


Lời giải:
Ta có:
$\sin B = \frac{AH}{AB}\Rightarrow AB=\frac{AH}{\sin B}=\frac{3}{\frac{3}{4}}=4$
$\sin B=\frac{3}{4}\Rightarrow \widehat{B}=48,6^0$
$\widehat{C}=90^0-\widehat{B}=90^0-48,6^0=41,4^0$