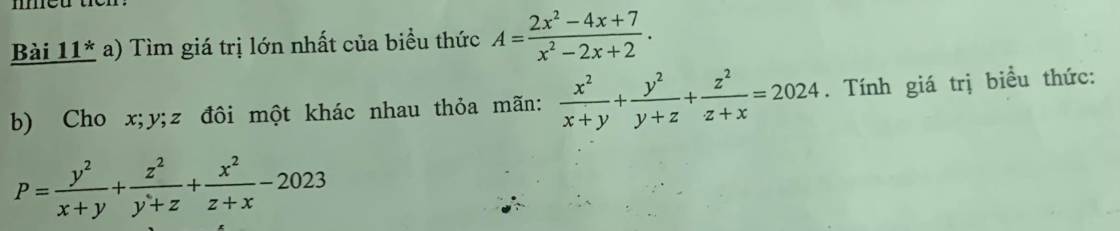a: \(A=\dfrac{2x^2-4x+7}{x^2-2x+2}\)

\(=\dfrac{2x^2-4x+4+3}{x^2-2x+2}\)

\(=2+\dfrac{3}{x^2-2x+2}=2+\dfrac{3}{\left(x-1\right)^2+1}\)

\(\left(x-1\right)^2+1>=1\forall x\)

=>\(\dfrac{3}{\left(x-1\right)^2+1}< =\dfrac{3}{1}=3\forall x\)

=>\(A=\dfrac{3}{\left(x-1\right)^2+1}+2< =3+2=5\forall x\)

Dấu '=' xảy ra khi x-1=0

=>x=1

\(B=x^{15}-8x^{14}+8x^3-8x^2+...-8x^2+8x-5\)

Vì \(x=7\) nên

\(x+1=8\)

\(B=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^3-\left(x+1\right)x^2+...-\left(x+1\right)x^2+\left(x+1\right)x-5\)

\(B=x^{15}-x^{15}-x^{14}+x^{14}+x^3-x^3-x^2+...-x^2+x^2+x-5\)

\(B=x-5\)

\(B=>7-5=2\)

Vậy \(B=2\)

Bài 4:

a: Xét ΔDHE vuông tại H và ΔDKF vuông tại K có

\(\widehat{HDE}\) chung

Do đó: ΔDHE~ΔDKF

b: ΔDHE~ΔDKF

=>\(\dfrac{DH}{DK}=\dfrac{DE}{DF}\)

=>\(\dfrac{2}{DK}=\dfrac{3}{5}\)

=>\(DK=2\cdot\dfrac{5}{3}=\dfrac{10}{3}\left(cm\right)\)

c: Xét ΔIKE vuông tại K và ΔIHF vuông tại H có

\(\widehat{KIE}=\widehat{HIF}\)(hai góc đối đỉnh)

Do đó: ΔIKE~ΔIHF

=>\(\dfrac{IK}{IH}=\dfrac{IE}{IF}\)

=>\(\dfrac{IK}{IE}=\dfrac{IH}{IF}\)

Xét ΔIKH và ΔIEF có

\(\dfrac{IK}{IE}=\dfrac{IH}{IF}\)

\(\widehat{KIH}=\widehat{EIF}\)(hai góc đối đỉnh)

Do đó: ΔIKH~ΔIEF

=>\(\widehat{IKH}=\widehat{IEF}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHBA~ΔABC

b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{ACB}\right)\)

Do đó ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HB\cdot HC=HA^2\)

c: Xét ΔADH vuông tại D và ΔAHB vuông tại H có

\(\widehat{DAH}\) chung

Do đó: ΔADH~ΔAHB

=>\(\dfrac{AD}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AD\cdot AB\left(1\right)\)

Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AE\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)

=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Xét ΔADE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔADE~ΔACB

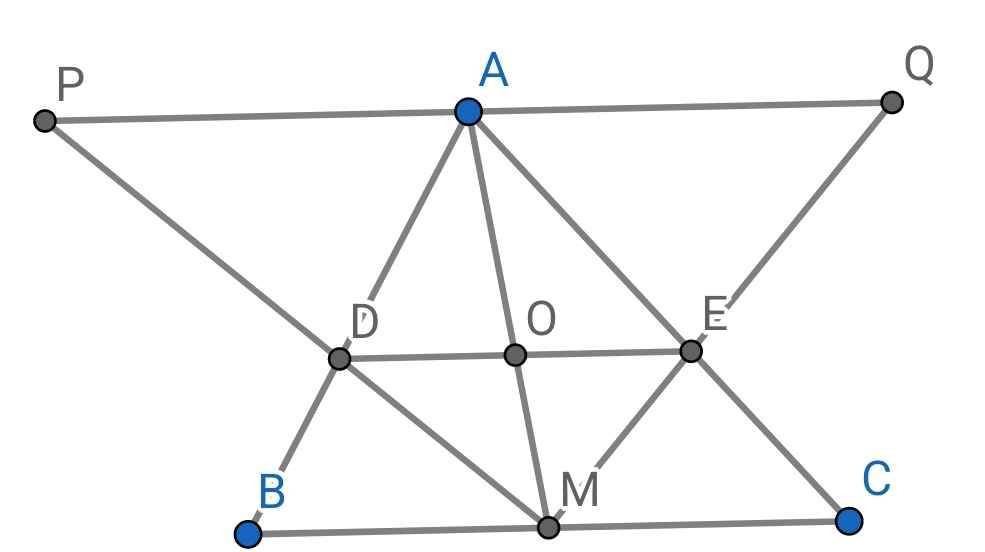
a) Do AM là đường trung tuyến của ∆ABC (gt)

⇒ M là trung điểm của BC

⇒ MB = MC

∆AMB có:

MD là tia phân giác của ∠AMB (gt)

⇒ AD/BD = AM/BM

∆AMC có:

ME là tia phân giác của ∠AMC (gt)

⇒ AE/CE = AM/MC

Mà MB = MC (cmt)

⇒ AD/BD = AE/CE

∆ABC có:

AD/BD = AE/CE (cmt)

⇒ DE // BC (định lý Thales đảo)

b) Do DE // BC (cmt)

⇒ DO // BM và OE // MC

∆ABC có:

DE // BC (cmt)

⇒ AD/AB = AE/AC

∆ABM có:

DO // BM (cmt)

⇒ AD/AB = OD/BM

∆ACM có:

OE // MC (cmt)

⇒ AE/AC = OE/MC

Mà AD/AB = AE/AC (cmt)

⇒ OD/BM = OE/MC

Mà MB = MC (cmt)

⇒ OD = OE

⇒ O là trung điểm của DE

c) Do PQ // BC (gt)

DE // BC (cmt)

⇒ DE // PQ

∆MPQ có:

DE // PQ (cmt)

⇒ DE/PQ = ME/MQ (1)

Do DE // PQ (cmt)

⇒ OE // AQ

∆MAQ có:

OE // AQ (cmt)

⇒ ME/MQ = MO/MA (2)

Từ (1) và (2) ⇒ DE/PQ = MO/MA

a: Xét ΔMAB có MD là phân giác

nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}=\dfrac{AM}{MC}\left(1\right)\)

Xét ΔAMC có ME là phân giác

nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)

Từ (1),(2) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)

Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)

nên DE//BC

b: Xét ΔABM có DO//BM

nên \(\dfrac{DO}{BM}=\dfrac{AO}{AM}\left(3\right)\)

Xét ΔAMC có OE//MC

nên \(\dfrac{OE}{MC}=\dfrac{AO}{AM}\left(4\right)\)

Từ (3),(4) suy ra \(\dfrac{DO}{BM}=\dfrac{OE}{MC}\)

mà MB=MC

nên DO=OE

=>O là trung điểm của DE

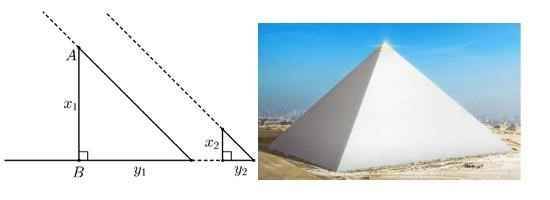
Do 2 tam giác vuông đồng dạng nên ta có:

\(\dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}\Rightarrow x_1=\dfrac{x_2.y_1}{y_2}=\dfrac{1.208,2}{1,5}=138,8\left(m\right)\)

Vậy kim tự tháp cao \(138,8\left(m\right)\)