Cho tam giác ABC không cân tại A. Đường tròn (O) thay đổi đi qua B và C theo thứ tự cắt AB, AC lần lượt tại M và N. Gọi P là giao điểm của BN và CM. Q là điểm chính giữa cung BC không chứa M,N của (O). K là tâm đường tròn nội tiếp tam giác PBC. CMR: KQ luôn đi qua 1 điểm cố định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có :
\(sin3x=sin\left(x+\frac{\pi}{4}\right)\Leftrightarrow\orbr{\begin{cases}3x=x+\frac{\pi}{4}+k2\pi\\3x=\pi-\left(x+\frac{\pi}{4}\right)+k2\pi\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{16}+\frac{k\pi}{2}\end{cases}}\) với k là số nguyên

để hàm số xác định với mọi x thuộc R thì
\(2m\cos^2x+\left(2-m\right)\cos x+4m-1\ge0\Leftrightarrow m\left(2cos^2x-cosx+4\right)\ge1-2cosx\)
mà \(2cos^2x-cosx+4>0\) nên :
\(m\ge\frac{1-2cosx}{2cos^2x-cosx+4}\)\(\Leftrightarrow\)\(m\ge max\left(\frac{1-2cosx}{2cos^2x-cosx+4}\right)=\frac{3}{7}\)
vậy điều kiện của m là : \(m\ge\frac{3}{7}\)




Gọi số thú săn đc mỗi ng là a1, a2,..., a7
vì mỗi người ăn đc số thú khác nhau nên giả sử là a1<a2<ả3<...<a7
TH1: a5>15⇒a5+a6+a7≥16+17+18=51>50a5>15⇒a5+a6+a7≥16+17+18=51>50
TH2 : a5≤15⇒a1+a2+a3+a4≤14+13+12+11=50⇒a5≤15⇒a1+a2+a3+a4≤14+13+12+11=50⇒a5+a6+a7≥50a5+a6+a7≥50

\(lim_{x\rightarrow0}\frac{7x^2}{ln\left(1+3x\right)}=lim_{x\rightarrow0}\frac{\left(7x^2\right)'}{\left(ln\left(1+3x\right)\right)'}=lim_{x\rightarrow0}\frac{14x}{\frac{3}{1+3x}}=0\)
(sử dụng quy tắc L'Hôpital)



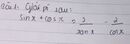
 ai đó giải giúp mình với ạ
ai đó giải giúp mình với ạ