Gọi độ dài quãng đường AB là x(km)

(Điều kiện: x>0)

Thời gian người đó đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)

Thời gian người đó đi từ B về A là \(\dfrac{x}{36}\left(giờ\right)\)

Thời gian đi ít hơn thời gian về là 10p=1/6 giờ nên ta có:

\(\dfrac{x}{36}-\dfrac{x}{40}=\dfrac{1}{6}\)

=>\(\dfrac{10x-9x}{360}=\dfrac{1}{6}\)

=>\(\dfrac{x}{360}=\dfrac{1}{6}\)
=>\(x=\dfrac{360}{6}=60\left(nhận\right)\)

vậy: Độ dài quãng đường AB là 60km

Gọi độ dài quãng đường AB là x (km) với x>0

Thời gian xe đi từ A đến B là: \(\dfrac{x}{40}\) giờ

Thời gian xe đi từ B về A là: \(\dfrac{x}{36}\) giờ

Do thời gian đi ít hơn thời gian về là 10 phút =1/6 giờ nên ta có pt:

\(\dfrac{x}{36}-\dfrac{x}{40}=\dfrac{1}{6}\)

\(\Leftrightarrow x\left(\dfrac{1}{36}-\dfrac{1}{40}\right)=\dfrac{1}{6}\)

\(\Leftrightarrow\dfrac{x}{360}=\dfrac{1}{6}\)

\(\Rightarrow x=60\left(km\right)\)

Đề chính xác hơn là \(ab+bc+ca\le\dfrac{1}{3}\)

Ý a phải là tính diện tích của hộp quà chứ bạn đề bài làm gì cho chiều cao của hình chóp tam giác đâu mà tính thể tích

a: 15p=0,25 giờ

Vận tốc trung bình mà Lan đi xe đạp từ nhà đến trường là:

1,8:0,25=7,2(km/h)

b: Thời gian còn lại là 15-1,5=13,5(phút)=0,225(giờ)

vận tốc Lan cần phải đi là:

1,8:0,225=8(km/h) 

a: Xét ΔAHN vuông tại N và ΔACH vuông tại H có

\(\widehat{HAN}\) chung

Do đó: ΔAHN~ΔACH

b: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có

\(\widehat{MAH}\) chung

Do đó: ΔAMH~ΔAHB

=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AM\cdot AB\)

=>\(AM\cdot15=12^2=144\)

=>AM=9,6(cm)

c: ΔANH~ΔAHC

=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AN\cdot AC\)

=>\(AM\cdot AB=AN\cdot AC\)

=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(HB=\sqrt{15^2-12^2}=9\left(cm\right)\)

ΔAHC vuông tại H

=>\(HA^2+HC^2=AC^2\)

=>\(HC=\sqrt{13^2-12^2}=5\left(cm\right)\)

BC=BH+CH=9+5=14(cm)

Xét ΔAMN và ΔACB có

\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

\(\widehat{MAN}\) chung

Do đó: ΔAMN~ΔACB

=>\(\dfrac{MN}{CB}=\dfrac{AM}{AC}\)

=>\(\dfrac{MN}{14}=\dfrac{9.6}{13}\)

=>\(MN=\dfrac{672}{65}\left(cm\right)\)

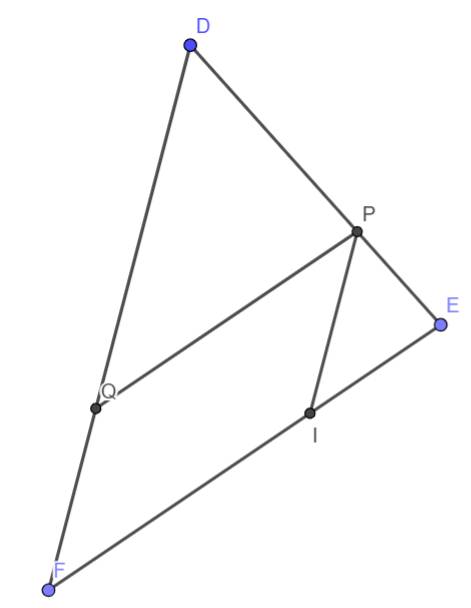
a) Ta có:

\(\dfrac{DP}{DE}=\dfrac{4}{6}=\dfrac{2}{3}\)

\(\dfrac{DQ}{DF}=\dfrac{6}{9}=\dfrac{2}{3}\)

\(\Rightarrow\dfrac{DP}{DE}=\dfrac{DQ}{DF}=\dfrac{2}{3}\)

\(\Delta DEF\) có:

\(\dfrac{DP}{DE}=\dfrac{DQ}{DF}=\dfrac{2}{3}\) (cmt)

\(\Rightarrow PQ\) // \(EF\)

\(\Rightarrow\widehat{DPQ}=\widehat{DEF}\) (đồng vị)

Xét \(\Delta DPQ\) và \(\Delta DEF\) có:

\(\widehat{D}\) chung

\(\widehat{DPQ}=\widehat{DEF}\) (cmt)

\(\Rightarrow\Delta DPQ\) ∽ \(\Delta DEF\) (g-g)

b) Sửa đề: Chứng minh \(\Delta EIP\) ∽ \(\Delta PQD\)

Do \(PQ\) // \(EF\) (cmt)

\(\Rightarrow PQ\) // \(FI\)

Do \(PI\) // \(DF\) (gt)

\(\Rightarrow PI\) // \(QF\)

Tứ giác \(FIPQ\) có:

\(PQ\) // \(FI\left(cmt\right)\)

\(PI\) // \(QF\) (cmt)

\(\Rightarrow FIPQ\) là hình bình hành

Do PI // QF (cmt)

\(\Rightarrow\widehat{PIE}=\widehat{QFI}\) (đồng vị)

Do PQ // EF (cmt)

\(\Rightarrow\widehat{DQP}=\widehat{QFI}\) (đồng vị)

Mà \(\widehat{PIE}=\widehat{QFI}\left(cmt\right)\)

\(\Rightarrow\widehat{PIE}=\widehat{DQP}\)

Do PQ // EF (cmt)

\(\Rightarrow\widehat{PEI}=\widehat{DPQ}\) (đồng vị)

Xét \(\Delta EIP\) và \(\Delta PQD\) có:

\(\widehat{PIE}=\widehat{DQP}\) (cmt)

\(\widehat{PEI}=\widehat{DPQ}\left(cmt\right)\)

\(\Rightarrow\Delta EIP\)  ∽ \(\Delta PQD\left(g-g\right)\)

a: Xét ΔDEF có

DA,FC là các đường cao

DA cắt FC tại H

Do đó: H là trực tâm của ΔDEF

=>EH\(\perp\)DF tại B

b: Xét tứ giác DCHB có \(\widehat{DCH}+\widehat{DBH}=90^0+90^0=180^0\)

nên DCHB là tứ giác nội tiếp

Xét tứ giác AFBH có \(\widehat{FAH}+\widehat{FBH}=90^0+90^0=180^0\)

nên AFBH là tứ giác nội tiếp

Ta có: \(\widehat{CBH}=\widehat{CDH}\)(DCHB nội tiếp)

\(\widehat{ABH}=\widehat{AFH}\)(AFBH nội tiếp)

mà \(\widehat{CDH}=\widehat{AFH}\left(=90^0-\widehat{CEF}\right)\)

nên \(\widehat{CBH}=\widehat{ABH}\)

=>BE là phân giác của góc ABC

Đề bài thiếu rồi em, ko có độ dài BC thì ko thể chứng minh tam giác này vuông

Giúp em với thầy