(x – 3) (2x +4) =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với mọi a;b;c ta có
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge2\left(a+b+c\right)-3\) (1)
Lại có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\Leftrightarrow6a^2+6b^2+6c^2\ge6ab+6bc+6ca\) (2)
Cộng vế (1) và (2):
\(7\left(a^2+b^2+c^2\right)\ge2\left(a+b+c+3ab+3bc+3ca\right)-3=2.12-3=21\)
\(\Rightarrow a^2+b^2+c^2\ge3\)
Dấu "=" xảy ra khi \(a=b=c=1\)

\(\dfrac{x-3}{x^2-x+1}-\dfrac{1}{x+1}+\dfrac{4x+4}{x^3-1}\)
\(=\dfrac{\left(x-3\right)\left(x+1\right)}{\left(x^2-x+1\right)\left(x+1\right)}-\dfrac{x^2-x+1}{\left(x^2-x+1\right)\left(x+1\right)}+\dfrac{4x+4}{\left(x^2-x+1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+x-3x-3-x^2+x-1+4x+4}{\left(x^2-x+1\right)\left(x+1\right)}\)
\(=\dfrac{3x}{\left(x^2-x+1\right)\left(x+1\right)}\)
\(=\dfrac{3x}{x^3+1}\)

a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH~ΔBDA
ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{4^2+3^2}=5\left(cm\right)\)
ΔADH~ΔBDA
=>\(\dfrac{AH}{BA}=\dfrac{AD}{BD}\)
=>\(AH=\dfrac{AB\cdot AD}{BD}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(AB//CD)
Do đó: ΔAHB~ΔBCD
=>\(\dfrac{BH}{CD}=\dfrac{AB}{BD}\)
=>\(BH\cdot BD=AB\cdot CD=CD^2\)


∆OAB vuông tại O
⇒ AB² = OA² + OB² (Pythagore)
= 3² + 4²
= 25
⇒ AB = 5
⇒ Chu vi ∆OAB:
OA + OB + AB = 3 + 4 + 5 = 12

Gọi H là giao điểm của BA và CK
Xét ΔBHC có
BK,CA là các đường cao
BK cắt CA tại D
Do đó: D là trực tâm của ΔBHC
=>HD\(\perp\)BC tại M
Xét ΔBMD vuông tại M và ΔBKC vuông tại K có
\(\widehat{MBD}\) chung
Do đó: ΔBMD~ΔBKC
=>\(\dfrac{BM}{BK}=\dfrac{BD}{BC}\)
=>\(BD\cdot BK=BM\cdot BC\)
Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
\(\widehat{MCD}\) chung
Do đó: ΔCMD~ΔCAB
=>\(\dfrac{CM}{CA}=\dfrac{CD}{CB}\)
=>\(CA\cdot CD=CM\cdot CB\)
\(BD\cdot BK+CD\cdot CA\)
\(=BM\cdot BC+CM\cdot BC=BC^2=4\cdot CQ^2\)

Diện tích đáy của 1 hộp quà là:
\(400:\dfrac{1}{3}:12=100\left(cm^2\right)\)
Độ dài cạnh đáy của hộp quà là:
\(\sqrt{100}=10\left(cm\right)\)
Diện tích giấy mà bạn An cần để làm 10 hộp quà đó là:
\(10\cdot\left[\dfrac{1}{2}\cdot\left(10\cdot4\right)\cdot13\right]=2600\left(cm^2\right)\)

\(\dfrac{x-1}{2}+\dfrac{x+1}{15}-\dfrac{2x-13}{6}=0\)
\(\Leftrightarrow\dfrac{15\left(x-1\right)}{30}-\dfrac{2\left(x+1\right)}{30}-\dfrac{5\left(2x-13\right)}{30}=0\)
\(\Leftrightarrow15\left(x-1\right)-2\left(x+1\right)-5\left(2x-13\right)=0\)
\(\Leftrightarrow15x-15-2x-2-10x+65=0\)
\(\Leftrightarrow3x+48=0\)
\(\Leftrightarrow x=-16\)


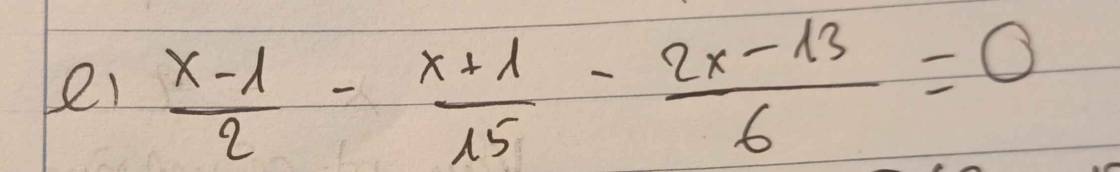
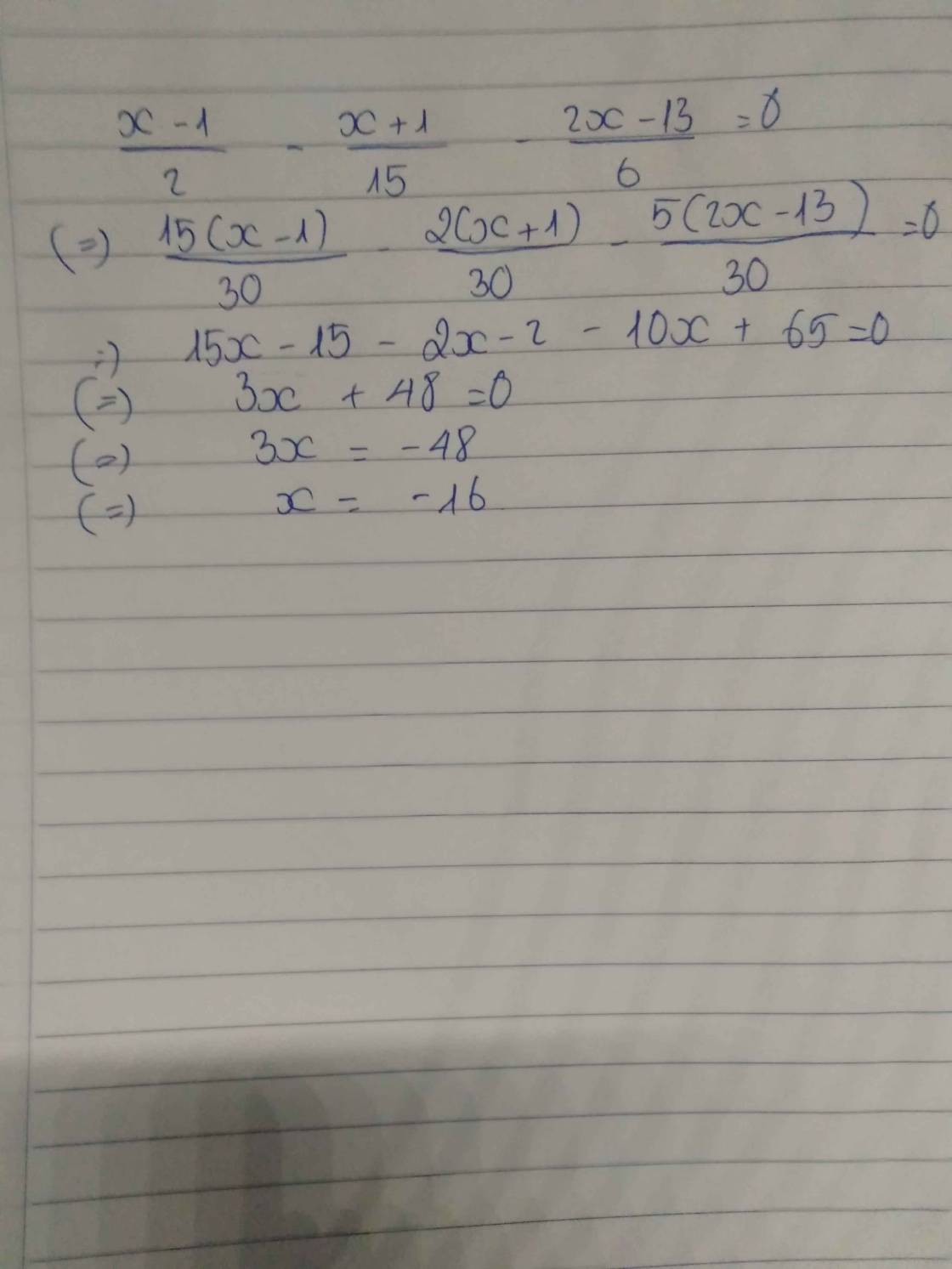
\(\left(x-3\right)\left(2x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
\(\left(x-3\right)\)\(\left(2x-4\right)\)\(=\) \(0\)
\(\Rightarrow\) \(\left(x-3\right)\)\(=\) \(0\) hoặc \(\left(2x-4\right)\)\(=\) \(0\)
\(TH1:\) \(\left(x-3\right)\)\(=\) \(0\)
\(x\) \(=\) \(0\) \(+\) \(3\)
\(x\) \(=\) \(3\)
\(TH2:\) \(\left(2x+4\right)\)\(=\) \(0\)
\(2x\) \(=\) \(0\) \(-\) \(4\)
\(2x\) \(=\) \(-4\)
\(x\) \(=\) \(-4\) \(:\) \(2\)
\(x\) \(=\) \(-2\)
Vậy \(x\) \(\in\) { \(3\) \(;\) \(-2\) }