Ta có

\(\frac{a+b+c}{2}=\frac{a+b-2}{c}=\frac{b+c+1}{a}=\frac{c+a+1}{b}=\frac{2\left(a+b+c\right)}{a+b+c}=2\)

Ta có

\(\frac{a+b+c}{2}=\frac{a+b-2}{c}=\frac{c+2}{2-c}=2\)

\(\Rightarrow c=\frac{2}{3}\)

\(\frac{a+b+c}{2}=\frac{c+a+1}{b}=\frac{b-1}{2-b}=2\)

\(\Rightarrow b=\frac{5}{3}\)

\(\frac{a+b+c}{2}=\frac{b+c+1}{a}=\frac{a-1}{2-a}=2\)

\(\Rightarrow a=\frac{5}{3}\)

\(a,b,c\ne o\)

VA \(a+b+c\ne o\)

LÀ HAI ĐIỀU KIỆN HOÀN TOÀN KHÁC NHAU VẬY MÀ ALIBABA XEM NHƯ LÀ MỘT.

nối M với h, ta có: 
MH = AC/2 = MC ( trung tuyến = 1/2 cạnh huyền của tam giác vuông AHC) 
=> MHC^ = MCH^ = 2.KCH^ ( vì CK là phân giác của ACB^) 
gt: KB = KC => KCH^ = KBH^ 
=> MHC^ = 2.KBH^ = KBH^ + KBH^ (1) 
mắt khác: 
MHC^ = KBH^ + KMH^ (2) ( góc ngoài và trong của tam giác BMH) 
(1) và (2) => KBH^ = KMH^ => BHM cân tại H => HB = HM (1) 
tổng góc trong của tam giác BMH là: 
KBH^ + BHA^ + AHM^ + KMH^ = 180* 
=> 2.KBH^ + 90* + AHM^ = 180* 
=> 2.KBH^ + AHM^ = 90* (2) 
tam giác AHC vuông => MAH^ + MCH^ = 90* 
=> MAH^ + 2.KCH^ = 90* 
=> MAH^ + 2.KBH^ = 90* (3) ( vì KCH^ = KBH^) 
(2) và (3) => AHM^ = MAH^ => HA = HM 
mặt khác: HM = AC/2 = AM 
=> HA = HM = AM => AHM là tam giác đều => HA = HM (4) 
(1) và (4) => HA = HB 
=> AHM là tam giác đều => MAH^ = 60* => ACB^ = 30* 
=> ABC^ = 180* - BAC^ - ACB^ = 180* - 105* - 30* = 45* 
(hoặc ABC^ = ABH^ = 45* => ACB^ = 30*)

Vẽ nháp bằng tay, hình không đẹp cho lắm :v Bài viết có hơi lỗi.

Bài toán phụ : Chứng minh tam giác vuông có 1 góc 60 độ thì cạnh góc vuông nhỏ hơn sẽ bằng 1 nửa cạnh huyền.

Tam giác MNP vuông tại M có góc N là 60 độ.

Trên tia đối tia MN lấy điểm Q sao cho MQ=MN

Tam giác NPQ có PM vừa là trung tuyến vừa là đường cao nên cân tại P, mà lại có 1 góc 60 độ nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều), từ đó suy ra NQ = NP, mà NQ= 2MN nên MN = \(\frac{1}{2}\)NP, bài toán được chứng minh.

Tương tự với bài toán của chúng ta :

\(\Delta ABC\)vuông tại Acó \(\widehat{B}=60^o\) \(\Rightarrow AB=\frac{1}{2}BC\)

\(\Delta ABH\)vuông tại H có \(\widehat{B}=60^o\) \(\Rightarrow HB=\frac{1}{2}AB\)

\(\Rightarrow HB=\frac{1}{4}BC\)

Trước hết \(\Delta ABH\) vuông tại H có \(\widehat{B}=60^o\)

 nên \(\widehat{HAB}=90^o-60^o=30^o\)Mà \(\widehat{DAH}+\widehat{HAB}=\widehat{BAC}=90^o\)

\(\Rightarrow\widehat{DAH}=60^o\)

\(\Delta DAH\)cân tại A ( AD = AH ), có góc DAH là 60^o nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều )

Như vậy AI là đường cao đồng thời cũng là phân giác góc DAH

\(\Rightarrow\widehat{IAH}=\frac{1}{2}\widehat{DAH}=\frac{60^o}{2}=30^o\)

\(\Rightarrow\widehat{KAB}=\widehat{IAH}+\widehat{HAB}=30^o+30^o=60^o\)

\(\Delta KAB\)có \(\widehat{KAB}=\widehat{KBA}=60^o\) nên là tam giác đều

\(\Rightarrow KB=AB\)

Mà \(HB=\frac{1}{2}AB\Rightarrow HB=\frac{1}{2}KB\), hay H là trung điểm của KB.

Vậy ....

dung roi

Tâm hồn con người xứ huế được bộc lộ là đẹp tâm hồn con người xứ huế là sự hòa quyện,tình đời,tình yêu quê hương đất nước bao la nồng  hậu,khát khoa,hoài vọng thiết tha

Học tốt nha bạn

abcabcabc

Với mọi đa thức f(x),khi khai triển luôn có dạng : a_n.xⁿ + a_{n - 1}.x^{n - 1} + a_{n - 2}.x^{n - 2} + ... + a₂.x² + a₁.x + a₀

\(\Rightarrow f\left(1\right)=a_n+a_{n-1}+a_{n-2}+...+a_2+a_1+a_0\)là tổng các hệ số của f(x)

Đặt đa thức đã cho là f(x) thì tổng các hệ số của f(x) khi bỏ dấu ngoặc trong biểu thức (khai triển) là :

f(1) = (3 - 4 + 1)²⁰⁰⁶.(3 + 4 + 1)²⁰⁰⁷ = 0²⁰⁰⁶.7²⁰⁰⁷ = 0

Để làm được bài này bạn phải đặt x=1 là tính tổng được hệ só nhé bạn

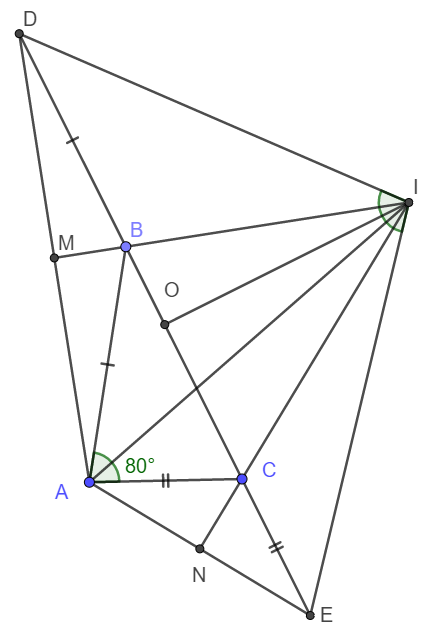
a) Ta có MD = MA; BD  BA nên MB là trung trức của AD.

Vậy nên I thuộc trung trực AD hay ID = IA.

Tương tự IE = IA.

Suy ra ID = IE hay tam giác IDE là tam giác cân tại I.

Lại có IO là trung tuyến nên OI là đường cao hay \(IO\perp DE\) 

b) Ta có \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}=180^o-80^o=100^o\)

\(\Rightarrow\widehat{ADB}+\widehat{AFC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}=\frac{100^o}{2}=50^o\)

\(\Rightarrow\widehat{DAB}+\widehat{EAC}=50^o\)

\(\Rightarrow\widehat{DAE}=80^o+50^o=130^o\)

Ta thấy \(\widehat{IDA}=\widehat{IAD};\widehat{IEA}=\widehat{IAE}\Rightarrow\widehat{IDA}+\widehat{IAE}=\widehat{IAD}+\widehat{IEA}=\widehat{DAE}=130^o\)

\(\Rightarrow\widehat{DIE}=360^o-130^o-130^o=100^o\)

Ta thấy ngay \(\widehat{MIN}=\widehat{MIA}+\widehat{NIA}=\frac{\widehat{DIA}}{2}+\frac{\widehat{EIA}}{2}=\frac{100^o}{2}=50^o\)

Bài bạn đấy nhìn khó hiểu???

khi đó tổng này sẽ phụ thuộc vào hiệu 2 ẩn nào đó, tuỳ theo mỗi trường hợp

thử chia đi, mình đúng cho ,mình mọt sách

Ta có: \(AC-AB>CK-BH\)    (*)

\(\Leftrightarrow AC+BH>AB+CK\)

\(\Leftrightarrow\left(AC+BH\right)^2>\left(AB+CK\right)^2\)

\(\Leftrightarrow AC^2+BH^2+2.AC.BH>AB^2+CK^2+2.AB.CK\)

\(\Leftrightarrow AC^2+BH^2+4S_{ABC}>AB^2+CK^2+4S_{ABC}\)

\(\Leftrightarrow AC^2+BH^2>AB^2+CK^2\)

\(\Leftrightarrow AK>AH\)  (**)

Xét tam giác ABC có \(\widehat{B}>\widehat{C}\Rightarrow AC>AB\)

Trên AC lấy điểm B' sao cho AB' = AB \(\Rightarrow AB'< AC\Rightarrow\) B' nằm giữa A và C.  (1)

Kẻ B'K' vuông góc AB tại K'.Suy ra B'K' // KC   (2)

Từ (1) và (2) suy ra K' nằm giữa A và K hay AK' < AK

Ta thấy ngay \(\Delta ABH=\Delta ACK'\)  (Cạnh huyền - góc nhọn) 

\(\Rightarrow AH=AK'\Rightarrow AK>AH\)

Vậy (**) đúng hay (*) đúng.

Ta có tam giác AKC vuông tại K

=> AC là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=>AC > CK

Ta có tam giác ABH vuông tại H

=> AB là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=> AB > BH

 Có: AC>CK;

AB>BH (cmt)

=> AC-AB > CK-BH

Ta có:

\(\frac{a_1}{a_2}=\frac{a_2}{a_3};\frac{a_2}{a_3}=\frac{a_3}{a_4};...;\frac{a_{2015}}{a_{2016}}=\frac{a_{2016}}{a_{2017}}\)

\(\Rightarrow\frac{a_1}{a_2}=\frac{a_2}{a_3}=...=\frac{a_{2016}}{a_{2017}}=k\)

\(\Rightarrow\frac{a_1^{2016}}{a_2^{2016}}=\frac{a_2^{2016}}{a_3^{2016}}=...=\frac{a_{2016}^{2016}}{a_{2017}^{2016}}=\frac{a_1^{2016}+a_2^{2016}+...+a_{2016}^{2016}}{a_2^{2016}+a_3^{2016}+...+a_{2017}^{2016}}=k^{2016}\left(1\right)\)

Ta lại có: 

\(k^{2016}=\frac{a_1}{a_2}.\frac{a_2}{a_3}...\frac{a_{2016}}{a_{2017}}=\frac{a_1}{a_{2017}}\left(2\right)\)

Từ (1) và (2) \(\frac{a_1^{2016}+a_2^{2016}+...+a_{2016}^{2016}}{a_2^{2016}+a_3^{2016}+...+a_{2017}^{2016}}=\frac{a_1}{a_{2017}}\)

Ta kéo dài tia MA , lấy điểm N thuộc tia MA sao cho IN = IK

Dễ thấy OAMB là hình vuông vì có góc O = góc B = góc A = 90⁰ và OM là tia phân giác góc O . => OA = OB

Ta có :  IN = IK (dựng hình) ; \(\widehat{NIO}=\widehat{OIK}\) (gt) ; IO là cạnh chung của hai tam giác NIO và OIK

=> \(\Delta NIO=\Delta IOK\left(c.g.c\right)\)=> \(\widehat{NOI}=\widehat{IOK}\) ; ON = OK

Xét hai tam giác vuông : \(\Delta AON\) và \(\Delta BOK\)có  OA = OB (cmt) ; ON = OK (cmt)  

=> \(\Delta AON=\Delta BOK\left(ch.cgv\right)\) => \(\widehat{AON}=\widehat{BOK}\)

Mà \(\widehat{BOK}+\widehat{AOK}=90^o\) \(\Rightarrow\widehat{AON}+\widehat{AOK}=90^o\)

hay \(\widehat{NOK}=2\widehat{IOK}=90^o\Rightarrow\widehat{IOK}=\frac{90^o}{2}=45^o\)

Cô ghi dấu góc ở đâu vậy