Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
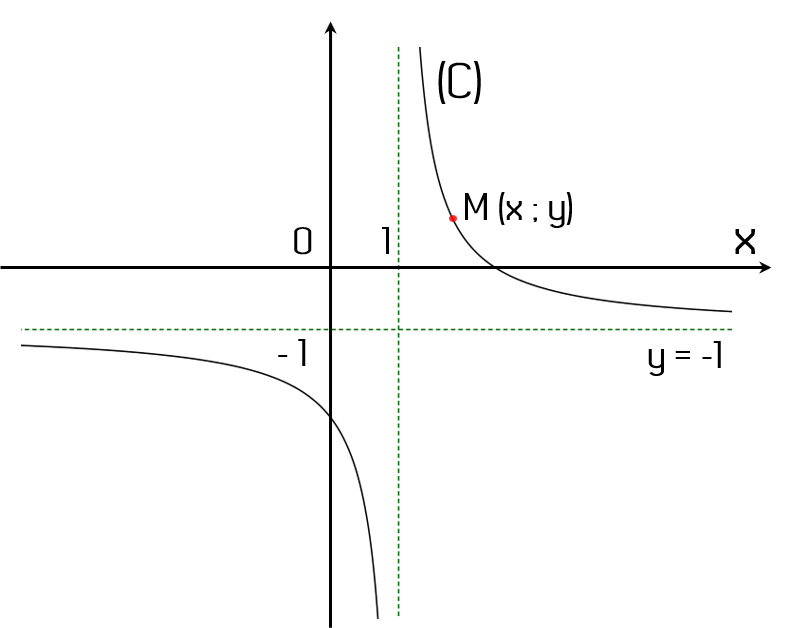
Khi hoành độ x của điểm M tiến tới −∞ thì giá trị y=f(x)
dần tới −∞.
dần tới +∞.
dần tới 0.
dần tới −1.
Câu 2 (1đ):
x→+∞limx+2x−1 bằng
+∞.
−2.
1.
−21.
Câu 3 (1đ):
x→−2+limx+2x−1 bằng
+∞.
−∞.
1.
−2.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào mừng game đã quay trở lại với
- khóa học Toán lớp 12 chính chàng khoảng
- lab.vn
- tiếp tục với nội dung của trường một thì
- ở Ban đầu chúng ta lần lượt Tìm hiểu về
- sự đồng biến nghịch biến cực đại cực
- tiểu cũng như giá trị lớn nhất nhỏ nhất
- của các hàm số thì sang bài 4 là một nội
- dung hoàn toàn mới liên quan tới đồ thị
- hàm số đó là đường tiệm cận
- ở trên lý thuyết thì sẽ có 3 loại được
- tiếp cận đó là chỉ cần đứng tiệm cận
- ngang và mình thì cũng xuyên Tuy nhiên
- nội dung chương trình của chúng ta sẽ
- chỉ tìm hiểu hai loại đó là tiệm cận
- ngang và tiệm cận đứng bây giờ thầy và
- kem sẽ đi vào loại đầu tiên đó là đường
- tiệm cận ngang
- trước khi tìm hiểu tiệm cận ngang là như
- thế nào khi thấy có hỏi chấm 1 để chúng
- ta đưa ra nhận xét về tiệm cận ngang Cho
- hàm số y bằng hai chữ x trên x trừ 1 có
- đồ thị C
- khi đó xét một điểm M bất kì thuộc vào
- đổi điểm số này các em hãy nhận xét cho
- thầy khoảng cách từ điểm M đến đường
- thẳng y = -1
- khi y = -1 là đường led nằm ngang này
- khi mà thầy cho ích Tiến dần tới dương
- vô cùng hoặc là âm cuối cùng
- Em hãy để có cái nhìn chứ còn hơn cái
- này còn phát ở trên Cảnh này ở đây thì
- đang có đồ thị C của hàm số pha điểm màu
- đỏ này là điểm M có tọa độ x y x là giá
- trị ở trong không phải đây là giá trị
- của y khi đó các em hãy quan sát sự thay
- đổi tung độ của điểm M Nếu như thầy cho
- giá trị của x Tiến dần tới âm vô cùng
- trong khi đó giá trị
- x càng dần tổ ấm cuối cùng khi phong độ
- của điểm Ờ sẽ càng dần tới 1 giá trị đó
- chính là giá trị 1
- 32 khoảng cách từ điểm M đến đường thẳng
- lên đứng màu xanh phía bên trên này
- chính là đường thẳng y = 51 sẽ ngày càng
- nhỏ đi và rất gần từ giá trị 0
- lý do đỏ chúng ta sẽ có nhận xét khi mà
- ích càng tiến tới âm vô cùng là riêng vô
- cùng thì cũng tương tự khoảng cách của
- điểm M đến đường thẳng y = -1 Hãy gần
- bằng 0 hay nói cách khác công độ của
- điểm M khi đó dẫn tới âm 12 như quan sát
- trên đồ thị này nếu ta kéo sai rồi vị về
- phía dương vô cùng thì đồ thị hàm số và
- đường thẳng bằng -1 sẽ ngày càng sát lại
- nhau rất gần nhau và tất nhiên đô thị
- thành phố hoa điện thoại gì bằng ra một
- sẽ không cắt nhau tại điểm nào khi đó
- nghĩ = -1 chính là hình ảnh đường tiệm
- cận ngang của đồ thị hàm số
- em im Tiến dần F1 nói theo ngôn ngữ giới
- hạn ta sẽ có giới hạn của Y khi X Tiến
- Dương vô cùng = -1 hoặc giới hạn của Y
- khi X Tiến Đạt âm vô cùng cũng mặc ở một
- thì y = -1
- đó chính là đường tiệm cận ngang của đồ
- thị hàm số từ Nhật xe đó thầy và các em
- sẽ đi vào định nghĩa của đường tiệm cận
- ngang Cho hàm số y bằng FX xác định trên
- một khoảnh khô hạn đường thẳng y = y0
- được gọi là đường tiệm cận ngang của đồ
- thị hàm số y bằng FX thêm chút đường
- tiệm cận ngang thì của đồ thị hàm số nếu
- như ít nhất một trong các điều kiện sau
- thì thỏa mãn điều kiện đầu tiên giới hạn
- Quản số khí X tiến ra âm vô cùng bằng y0
- học Điều kiện thứ hai giới hạn Quảng số
- khí X tiến ra dương vô cùng bằng ý không
- ít nhất một trong các điều kiện có nghĩa
- là nếu như thỏa mãn điều kiện này hoặc
- điều kiện này thì chúng ta bù Để kết
- luôn vì đường tiệm cận ngang
- Ừ nếu như thỏa mãn cả hai điều kiện thì
- lại càng tốt con không thỏa mãn bất cứ
- điều kiện nào thì đi bằng ý không không
- là đường tiệm cận ngang của đồ thị hàm
- số
- và chú rể đều cho thấy khoảng vô hạn sẽ
- có dạng là a dương vô cùng âm vô cùng B
- hoặc là âm vô cùng dương vô cùng
- Ai biểu diễn của đường tiệm cận ngang ở
- trên hình ảnh sẽ như sau đây là đồ thị
- của hàm số y = FX trên hệ trục tọa độ
- nếu như ta cũng kéo dài mãi đồ thị của
- hàm số dùng nét về phía bên trái của chủ
- y thì đâu thì làm số này sẽ tiến tới rất
- gần đường thẳng y = ý không và không cắt
- đường thẳng này và giới hạn của hàm số
- khí X tiến ra âm mưu cùng khi đó bằng y0
- thì ta kết luận y = ý không đường nằm
- ngang này chính là đường tiệm cận ngang
- của đồ thị hàm số y bằng FX hay gọi tắt
- là tiệm cận ngang
- kể từ đó chúng ta sẽ đi vào ví dụ quay
- trở lại với đồ thị hàm số ở hỏi chấm 1
- nếu ta tính được giới hạn cảm số khí ích
- Tiến âm vô cùng = -1 hoặc giới hạn
- khoảng số ký ý kiến ra riêng vô cùng ở
- một thì đường thẳng y = 51 là một tiệm
- cận hàng của đổi điểm số thấp một ở đây
- chính là đi không như vậy để tìm tiệm
- cận ngang của đồ thị hàm số ta sẽ đi
- kiểm tra xem giới hạn quả xấu khí ít tín
- chấp vô cùng và Dương vô cùng sẽ dần tới
- giá trị nào nếu như một trong hai giới
- hạn này cho ta một giá trị khác âm vô
- cùng và trường cùng ta sẽ kết luận bằng
- y0 là đường tiệm cận ngang cho con Nếu
- không thỏa mãn điều này thì đồ thị hàm
- số sẽ không có điều gì cần anh nào cả
- cho ví dụ nhựa hỏi chấm 2 2 Cho hàm số y
- bằng x trừ 1 trên x cộng 2 có đồ thị c
- các em Hãy tìm tất cả các tiệm cận ngang
- của đồ thị hàm số trao giải nhất như
- chúng ta vừa đề cập các em sẽ cần thì
- tính giới hạn của hàm số ý ít tiền riêng
- cùng hoặc âm vô cùng ta phải tính cả hai
- giới hạn này ở đây thầy sẽ tính giới hạn
- thì ít tiền ra dương vô cùng trước nhé
- đề
- thi thấy có một thị trường riêng hướng
- dẫn cách để em tính giới hạn của các hàm
- số phân thức sạc như thế này hai đều ở
- ngay chưa có phải học chúng ta
- anh với hàm phân thức này ta sẽ chia cả
- tử và mẫu cho lũy thừa và cao nhất ở đây
- chính là ích ích ích Tiến Dương vô cùng
- kỳ 1 trên x sẽ bằng 0 và 2 trên x cũng
- bằng không nên Giới hạn chúng ta sẽ là
- một chiều một pha đặc thù bằng một như
- vậy chúng ta đã tìm được một giá trị
- không nên có thể kết luận về đường tiệm
- cận ngang nhưng đề bài Yêu cầu tìm tất
- cả rất có thể khi ít tiến âm cùng sẽ cho
- ta thế mua đường tiệm cận là nữa nên kem
- hệ tình thêm cho thầy giới hạn của hàm
- số khí x chỉ là âm cùng sẽ bằng bao
- nhiêu nhất
- Anh ta sẽ có giới hạn này cũng mặc một
- như vậy chúng ta sẽ trình bày cụ thể như
- sau Trước tiên là thật xác định a How to
- Yamaha hoa ta tính được giới hạn khí X
- Tiến ta dương vô cùng bằng một nên là
- kết luận đường thẳng y = 1 là tiệm cận
- ngang của đồ thị hàm số bên cạnh tiệm
- cận ngang thì loại Thứ hai chúng ta
- nghiên cứu đó là đường tiệm cận đứng hoa
- trở lại với hàm số bằng hai chữ x trên x
- trừ 1 Chúng ta lại tiếp tục đưa ra những
- nhận xét lần này là tung độ của điểm M
- khi mặt x Tiến dần tới 1 trở lại với
- hình ảnh Nếu như thầy kéo dài đô thị của
- hàm số C xuống phía bên dưới mãi như thế
- này khi kem có thể thấy đường nét đứt
- thẳng đứng này chính là đường thẳng x =
- 1 thì đồ thị C và đường thẳng này sẽ
- ngày càng phát lại nhau rất gần nhau khi
- đó ở nhánh đầu thị nằm phía bên trái
- đường thẳng x = 1 khi ta sẽ thấy tốc độ
- để mở khi mở càng di chuyển xuống phía
- bên dưới như thế này hãy có giá trị ngày
- càng nhỏ anh em cuối cùng con ở nhà thứ
- hai nhánh bên phải này chúng ta cũng làm
- tương tự kéo dài đồ thị lên phía trên và
- di chuyển điểm M trên đồ thị đấy ta sẽ
- thấy nếu như hoành độ mờ càng dần tới 1
- có nghĩa là đồ thị cảnh sát lại đường
- thẳng x = 1 thì tung động thì mời sẽ cứ
- tiếp tục tăng cho đến dương vô cùng như
- vậy ở mỗi nhánh của đô thị sẽ có những
- cái quả khác nhau và chúng ta có thể
- nhận xét nếu như điểm m ở nhà anh thì
- bên phải có nghĩa là nằm bên phải đường
- thảm x bằng 1 thì khi ích Tiến dần tới 1
- có nghĩa là tớ một cọc thì tung độ sẽ
- tiến dần ra thì vô cùng con thì ích Thì
- thấy 1 - có nghĩa nằm một nhánh phía thế
- này điểm M di chuyển trong kinh giới thì
- tốc độ điểm m sẽ dần ra âm vô cùng anh
- nói theo ngôn ngữ của giới hạn một bên
- sẽ là giới hạn của hàm số khí X tới một
- cậu là dư cuối cùng còn x tiến tới một
- chiều là âm vô cùng khi đó x bằng 1
- chính là hình ảnh của Đường tiệm cận
- đứng đồ thị hàm số C
- anh ta đi Bảo Định nghĩa cụ thể đường
- tiệm cận đứng cho đường thẳng x = x0
- đường thẳng này được gọi là đường tiệm
- cận đứng của đồ thị hàm số y bằng FX Nếu
- ít nhất một trong các điều kiện sau được
- mãn hai điều kiện đầu tiên là giới hạn
- Quảng tố khí X tiền tệ ích công cộng hay
- điều kiện tiếp theo là giới hạn Quảng số
- khi X tiền đấy không - Nếu như ít nhất
- một trong các điều kiện này cho ta kết
- quả là âm vô cùng hoặc dùng một cùng thì
- kết luận X = x0 là đường tiệm cận đứng
- của đồ thị hàm số con nếu tất cả các
- điều kiện này đều trả cho ta một giá trị
- khác âm vô cùng riêng một cùng khi đó x
- = 0 0 là đường tiệm cận đứng của nửa
- điểm xấu nhất ví dụ trên hình ảnh đây là
- đồ thị hàm số y = ax Nếu như ta kéo dài
- đầu điểm xấu về phía trên như thế này
- thì đô thị này sẽ gần sát tới đường
- thẳng x = 0 và không cắt lần này
- thế giới hạn của số khí X tiền lợi ích
- công cộng khi đó vẽ bằng dương một cùng
- thì X bằng những không được gọi là đường
- tiệm cận đứng gọi tắt là tiệm cận đứng
- của đồ thị hàm số y bằng FX Tuy nhiên ở
- đây lại phát sinh một vấn đề ít không là
- giá trị như thế nào chúng ta lấy ít
- không như thế nào để tính giới hạn này
- thì hiểu lâu ra chúng ta có thể nhớ mẹ
- như sau ít không chính là đầu của các
- khoảng xác định phải chú ý đến không
- thấy không là các giá trị âm vô cùng
- dương vô cùng
- cho nên thể dục trên khoảng tử 1 đến
- dương vô cùng thì đâu các khoảng xác
- định chính là một phản giữa vô cùng
- thế nhưng ít không khi đó chỉ nhận giá
- trị bằng một cụ thể chúng ta đến với ví
- dụ tiếp theo họ Trần bốn Cho hàm số y
- bằng x trừ 1 trên x cộng 2 có đồ thị c
- Tìm tất cả các tiệm cận đứng của đồ thị
- hàm số này Đầu tiên bước rất quan trọng
- tìm điều kiện xác định ở đây điều kiện
- xác định là d = r chửi em hay khi từ
- điều kiện xác định này chúng ta sẽ đi
- tìm các giá trị không để tính giới hạn
- và tình hình ảnh đứng hãy viết khoảng
- thì đây chính là từ âm vô cùng đến ấp 2
- hợp với khoảng từ âm hay cho đến dương
- vô cùng nên kém có thể thấy ít không ở
- đây ta chính là âm hay do đó tính cho
- thầy giới hạn của hàm số khí X tiến tới
- -2 +
- thế giới hạn này có kết quả là âm vô
- cùng nên ta có thể kết luận đường thẳng
- x = 2 là tiệm cận đứng của đồ thị hàm số
- hoặc các em có thể tính giới hạn khoảng
- số này thì ít tiền tưởng ấp 2 - cũng sẽ
- cho ta X và hai là tìm cận đúng như vậy
- chúng ta đã tìm hiểu xong về hai đường
- tiệm cận của hàm số tiệm cận ngang và
- tiệm cận đứng sau đây chúng ta đến với
- những ví dụ vận dụng tổng hợp cho cả
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022

