Vận tốc, gia tốc trong dao động điều hòa SVIP

I. Vận tốc của vật dao động điều hòa

Vận tốc tức thời của một vật được xác định bằng công thức: \(\text{v}=\dfrac{\Delta x}{\Delta t}\) với \(\Delta t\) rất nhỏ, tức là bằng độ dốc của đồ thị (\(x\) - \(t\)) tại điểm đang xét.

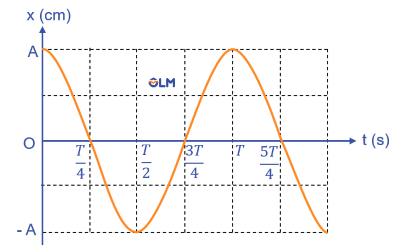
Xét vật có đồ thị dao động điều hòa như hình trên. Độ dốc của đồ thị, tức là vận tốc của vật, có giá trị cực đại khi ở vị trí cân bằng (VTCB) rồi giảm dần đến 0 khi vật ra đến vị trí biên. Sau đó độ dốc của đồ thị lại tăng dần đến giá trị cực đại khi vật về đến VTCB.

1. Phương trình của vận tốc

Một vật dao động điều hòa có phương trình li độ: \(x=A\cos\left(\omega t+\varphi\right)\)

Đạo hàm của li độ $x$ theo thời gian, kí hiệu là $x'$ chính là \(\text{v}=\dfrac{\Delta x}{\Delta t}\), suy ra ta có:

\(\text{v}=x'=-\omega A\sin\left(\omega t+\varphi\right)\) (1)

Công thức (1) chính là phương trình của vận tốc, có thể được viết thành:

\(\text{v}=\omega A\sqrt{1-\cos^2\left(\omega t+\varphi\right)}\)

Thay \(x=A\cos\left(\omega t+\varphi\right)\) vào ta được:

\(\text{v}=\pm\omega\sqrt{A^2-x^2}\)

• Khi vật ở vị trí cân bằng thì \(\text{v}=\pm\omega A\)
• Khi vật ở vị trí biên thì \(\text{v}=0\)

2. Đồ thị của vận tốc

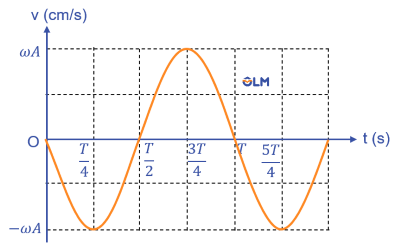
Hình trên là đồ thị vận tốc của một dao động điều hòa với \(\varphi\) = 0. Nó cũng là một đường hình sin.

II. Gia tốc của vật dao động điều hòa

Gia tốc tức thời của một vật được xác định bằng công thức: \(a=\dfrac{\Delta\text{v}}{\Delta t}\) với \(\Delta t\) rất nhỏ, tức là bằng độ dốc của đồ thị vận tốc tại điểm đang xét. Độ dốc của đồ thị ở Hình 2, hay gia tốc của vật, có giá trị bằng 0 khi vật ở vị trí cân bằng, rồi tăng đến giá trị cực đại khi vật ở vị trí biên.

1. Phương trình của gia tốc

Gia tốc tức thời của một vật là đạo hàm của vận tốc theo thời gian, kí hiệu là \(\text{v}'\).

\(a=\text{v}'=-\omega^2A\cos\left(\omega t+\varphi\right)\) (2)

Công thức (2) chính là phương trình của gia tốc.

Thay \(x=A\cos\left(\omega t+\varphi\right)\) vào ta được:

\(a=-\omega^2x\)  (3)

Từ công thức (3) ta thấy:

• Khi vật ở vị trí cân bằng: \(a=0\)
• Khi vật ở vị trí biên: \(a=\pm\omega^2A\)

2. Đồ thị của gia tốc

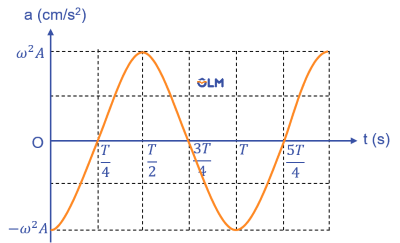
Hình trên là đồ thị của gia tốc (với \(\varphi\) = 0), nó cũng là một đường hình sin như li độ và vận tốc).

1. Phương trình của vận tốc và gia tốc của một vật dao động điều hòa có li độ là \(x=A\cos\left(\omega t+\varphi\right)\):

\(\text{v}=-\omega A\sin\left(\omega t+\varphi\right)\)

\(a=-\omega^2A\cos\left(\omega t+\varphi\right)\)

2. Đồ thị của vận tốc, gia tốc theo thời gian là đường hình sin. Vận tốc của vật dao động sớm pha \(\dfrac{\pi}{2}\) so với li độ, còn gia tốc của vật dao động ngược pha so với li độ.

3. Vectơ gia tốc luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ.

4. Tại vị trí biên, vận tốc của vật bằng 0, còn gia tốc của vật có độ lớn cực đại. Tại vị trí cân bằng, gia tốc của vật bằng 0 còn vận tốc của vật có độ lớn cực đại.