Tổng các góc trong một tam giác SVIP

Ta có định lí sau:

Tổng ba góc trong một tam giác bằng $180^{\circ}$.

Tổng ba góc trong một tam giác là tổng số đo ba góc trong tam giác đó.

Chứng minh định lí:

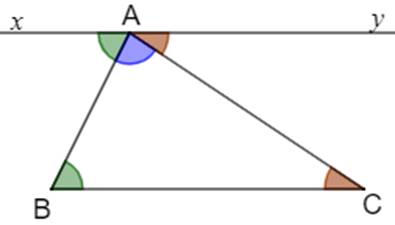
Qua A kẻ đường thẳng $xy$ song song với BC.

$xy$ // BC \(\Rightarrow\widehat{B}=\widehat{BAx}\), \(\widehat{C}=\widehat{CAy}\) (các cặp góc so le trong).

Do đó \(\widehat{A}+\widehat{B}+\widehat{C}=\widehat{BAC}+\widehat{BAx}+\widehat{CAy}=180^\circ\).

Ví dụ: Tìm số đo các góc chưa biết của các tam giác trong hình vẽ dưới đây.

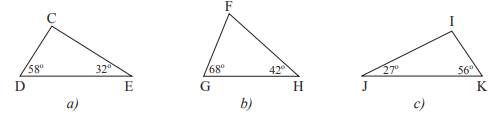
Giải

Áp dụng định lí về tổng số đo ba góc của tam giác, ta có:

a) \(\widehat{C}=180^\circ-32^\circ-58^\circ=90^\circ\).

b) \(\widehat{F}=180^\circ-68^\circ-42^\circ=70^\circ\).

c) \(\widehat{I}=180^\circ-27^\circ-56^\circ=97^\circ\).

Chú ý: Trong ví dụ trên:

- Tam giác FGH có ba góc đều nhọn nên gọi là tam giác nhọn.

- Tam giác IJK có một góc tù nên gọi là tam giác tù.

- Tam giác CDE có một góc vuông nên gọi là tam giác vuông. Trong tam giác CDE vuông tại C, CD và CE là hai cạnh góc vuông, DE là cạnh huyền.

Tam giác CDE có: \(\widehat{D}+\widehat{E}=58^\circ+32^\circ=90^\circ\).

Nhận xét: Hai góc có tổng bằng $90^{\circ}$ được gọi là hai góc phụ nhau. Trong tam giác vuông, hai góc nhọn phụ nhau. 

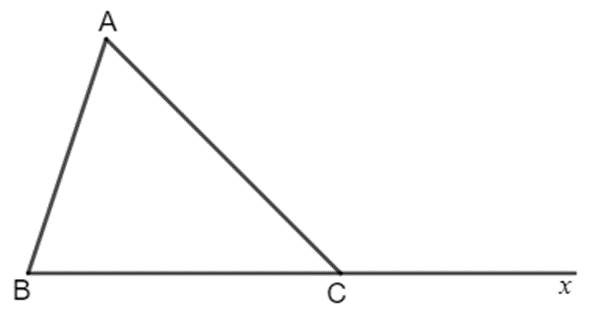
Góc ACx được gọi là góc ngoài tại C của tam giác ABC. Góc ACx không kề với hai góc A và B của tam giác ABC.

Mỗi góc ngoài của một tam giác có số đo bằng tổng số đo hai góc trong không kề với nó.