Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Mệnh đề phủ định của "20 là số hợp số" là

"20 là số tự nhiên".

"20 là số nguyên".

"20 không phải hợp số".

"20 là số hữu tỉ".

Câu 2 (1đ):

Trong các câu sau, câu nào không là mệnh đề?

n-1

là số lẻ.

Tổng ba góc trong một tam giác bằng

360^\circ

.

Hình vuông có hai đường chéo bằng nhau.

Gia Lộc là một huyện của tỉnh Hải Dương.

Câu 3 (1đ):

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp $K=\Big\{ x \in \mathbb{R}\, \big| \, |x| \le 3 \Big\}$ ta có

K=\left[ -3;3 \right]

.

K=\left(-\infty ;-3 \right] \cup \left[ 3;+\infty \right)

.

K=\left[ 3;+\infty \right)

.

K=\left(-3;3 \right)

.

Câu 4 (1đ):

Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned} & x+3y-6>0 \\ & 2|x|+y^2+4>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x<0 \\ & y\ge 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+3y^3<0 \\ & x+y \le 1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+2y-z>0 \\ & y<0 \\ \end{aligned} \right.

.

Câu 5 (1đ):

Điểm $A(-1;3)$ là điểm không thuộc miền nghiệm của bất phương trình nào sau đây?

2x-y+4<0

.

x+3y>0

.

-3x+2y-4<0

.

3x-y\le 0

.

Câu 6 (1đ):

Giá trị của biểu thức $A=\sin^2 15^\circ+\sin^2 75^\circ+\cos 120^\circ$ là

A=\dfrac{3}{2}

.

A=-\dfrac{3}{2}

.

A=\dfrac{1}{2}

.

A=-\dfrac{1}{2}

.

Câu 7 (1đ):

Cho tam giác $ABC$ với $BC=7$ cm, $AC=9$ cm, $AB=4$ cm. Giá trị $\cos A$ bằng

\dfrac{1}{3}

.

\dfrac{1}{2}

.

\dfrac{2}{3}

.

-\dfrac{2}{3}

.

Câu 8 (1đ):

Mệnh đề phủ định của "Hà Nội là thủ đô của nước Việt Nam" là

"Hà Nội là thành phố thuộc miền nam Việt Nam".

"Hà Nội là thành phố có diện tích lớn nhất Việt Nam".

"Hà Nội không phải là thủ đô của nước Việt Nam".

"Hà Nội là thành phố đông dân nhất Việt Nam".

Câu 9 (1đ):

Cho ba tập hợp $A=\left(-\infty ;0 \right]$ , $B=\left(1;+\infty \right)$ và $C=\left[ 0;1 \right)$ . Khi đó $\left(A\cup B \right) \cap C$ bằng

\varnothing

.

\mathbb{R}

.

\left\{ 0;1 \right\}

.

\left\{ 0 \right\}

.

Câu 10 (1đ):

Cho $A=\left\{ 0;1;2;3;4 \right\}, \, B=\left\{ 2;3;4;5;6 \right\}.$ Tập hợp $\left(A\backslash B \right)\cup \left(B\backslash A \right)$ bằng

\left\{ 5;6 \right\}.

\left\{ 0;1;5;6 \right\}.

\left\{ 2;3;4 \right\}.

\left\{ 1;2 \right\}.

Câu 11 (1đ):

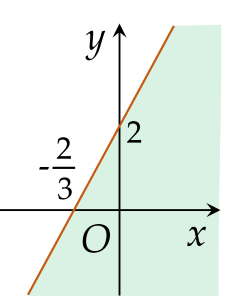
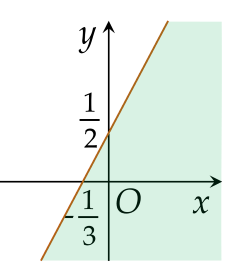
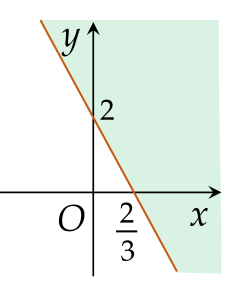
Phần không tô màu là hình vẽ biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?

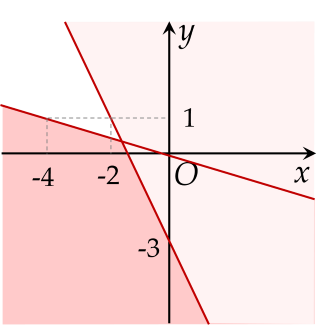
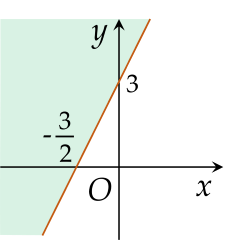
loading...

\left\{ \begin{aligned} & x+4y<0 \\ & 2x+y+3\le 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y\ge 0 \\ & 2x+y+3\ge 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y>0 \\ & 2x+y+3>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+4y>0 \\ & 2x+y+3\le 0 \\ \end{aligned} \right.

.

Câu 12 (1đ):

Miền nghiệm của bất phương trình sau $3x-2y+1\ge 0$ là phần tô màu (bao gồm cả đường thẳng) trong hình vẽ nào dưới đây?

Câu 13 (1đ):

Cho $A$ là tập hợp các học sinh lớp 10 đang học ở trường X và $B$ là tập hợp các học sinh đang học môn Tiếng Anh của trường X.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A\cap B$ là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường X.
b) $A\backslash B$ là tập hợp những học sinh lớp 10 và không học Tiếng Anh ở trường X.
c) $A\cup B$ là tập hợp các học sinh lớp 10 và học sinh học môn Tiếng Anh ở trường X.
d) $B \backslash A$ là tập hợp các học sinh học lớp 10 ở trường X nhưng không học môn Tiếng Anh.

Câu 14 (1đ):

Một công ty viễn thông tính phí $1$ $000$ đồng mỗi phút gọi nội mạng và $2$ $000$ đồng mỗi phút gọi ngoại mạng. Gọi $x$ và $y$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tổng đài luôn thấp hơn $100$ nghìn đồng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số tiền Bình phải trả cho cuộc gọi nội mạng mỗi tháng là $x$ (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là $2y$ (nghìn đồng) và $x \in \mathbb{N}, \, y\in \mathbb{N}$ .
b) $x+2y<100$ .
c) Nếu $50$ và $20$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng thì số tiền phải trả cho tổng đài thấp hơn $100$ nghìn đồng.
d) Nếu $50$ và $25$ lần lượt là số phút gọi nội mạng, ngoại mạng trong một tháng thì số tiền phải trả cho tổng đài vượt quá mục tiêu của Bình.

Câu 15 (1đ):

Cho $\sin \alpha =\dfrac{1}{3}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\cos^2 \alpha =\dfrac{8}{9}$ .
b) $A=\sin^2 \alpha + 3\cos^2 \alpha =\dfrac{35}{9}$ .
c) $B=5\sin^2 \alpha - \cos^2 \alpha =-\dfrac{1}{3}$ .
d) $C=\sqrt{\sin^2 \alpha + 3\cos^2 \alpha}+\sqrt{\cos^2 \alpha - 7\sin^2 \alpha}=2$ .

Câu 16 (1đ):

Lớp 10A có tất cả $40$ học sinh trong đó có $13$ học sinh chỉ thích đá bóng, $18$ học sinh chỉ thích chơi cầu lông và số học sinh còn lại thích chơi cả hai môn thể thao nói trên.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Có $9$ học sinh thích chơi cả hai môn cầu lông và bóng đá.
b) Có $22$ học sinh thích bóng đá.
c) Có $26$ học sinh thích cầu lông.
d) Có $21$ học sinh chỉ thích chơi một trong hai môn cầu lông và bóng đá.

Câu 17 (1đ):

Cho các tập hợp khác rỗng $A=\left(m-18;\,2m+7 \right)$ , $B=\left(m-12\,;\,21 \right)$ và $C=\left(-15\,;\,15 \right)$ . Có bao nhiêu giá trị nguyên của tham số $m$ để $A\backslash B\subset C$ ?

Trả lời:

Câu 18 (1đ):

Trong đợt quyên góp ủng hộ đồng bào miền Bắc bị lũ lụt năm 2024, có $25$ học sinh lớp 2A đã tham gia ủng hộ, mỗi học sinh ủng hộ nhiều nhất hai tờ tiền khác nhau trong ba loại tờ tiền mệnh giá $5$ $000$ đồng, $10$ $000$ đồng và $20$ $000$ đồng. Biết rằng số học sinh đã tham gia ủng hộ thỏa mãn đồng thời ba kết quả sau:

(1) Số học sinh chỉ ủng hộ một tờ $5$ $000$ đồng bằng tổng số học sinh chỉ ủng hộ một tờ $10$ $000$ đồng và số học sinh chỉ ủng hộ một tờ $20$ $000$ đồng.

(2) Trong số học sinh không ủng hộ tờ $5$ $000$ đồng thì số học sinh có ủng hộ tờ $10$ $000$ đồng nhiều gấp hai lần số học sinh có ủng hộ tờ $20$ $000$ đồng.

(3) Số học sinh chỉ ủng hộ một tờ $5$ $000$ đồng nhiều hơn số học sinh ủng hộ tờ $5$ $000$ đồng và một tờ khác là $1$ học sinh.

Có bao nhiêu học sinh lớp 2A chỉ ủng hộ một tờ $10$ $000$ đồng?

Trả lời:

Câu 19 (1đ):

Tìm các nghiệm $(x;y)$ của bất phương trình $\dfrac{x}{2}+\dfrac{y}{3}-1\le 0$ . Trong đó $x,y$ là các số nguyên dương. Tính $x + y$ .

Trả lời:

Câu 20 (1đ):

Một máy cán thép có thể sản xuất hai sản phẩm thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc $40$ giờ một tuần). Công suất sản xuất thép tấm là $250$ tấn/giờ, công suất sản xuất thép cuộn là $150$ tấn/giờ. Mỗi tấn thép tấm có giá $25$ USD, mỗi tấn thép cuộn có giá $30$ USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa $5$ $000$ tấn thép tấm và $3$ $500$ tấn thép cuộn. Cần sản xuất $m$ tấn thép tấm và $n$ tấn thép cuộn một tuần để lợi nhuận thu được là cao nhất. Tính $m - n$ .

Trả lời:

Câu 21 (1đ):

Miền biểu diễn nghiệm của hệ bất phương trình $\left\{ \begin{aligned} & y \ge -2 \\ & x \ge 2 \\ & 2x+y \le 8 \\ \end{aligned} \right.$ là một miền đa giác. Tính diện tích $S$ của đa giác đó.

Trả lời:

Câu 22 (1đ):

Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí $A$ .

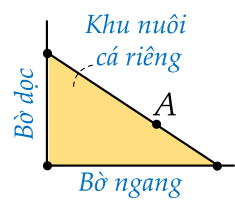
loading...

Diện tích nhỏ nhất có thể giăng là bao nhiêu $m^2$ , biết rằng khoảng cách từ cọc đến bờ ngang là $5$ m và khoảng cách từ cọc đến bờ dọc là $12$ m. (Làm tròn kết quả đến hàng đơn vị)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP