Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Sự đồng quy của ba đường trung trực trong tam giác SVIP
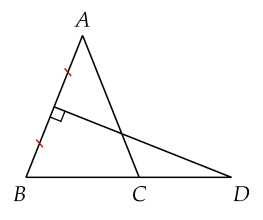
Cho ΔABC cân tại A, có A=50∘. Đường trung trực của AB cắt BC ở D. Số đo CAD là
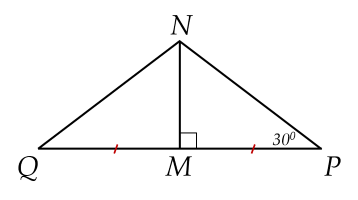
Cho ΔMNP vuông tại M có P=30∘. Trên tia đối của tia MP lấy điểm Q sao cho MQ=MP. Số đo NQM là

Cho xOy=40∘. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Lấy điểm C sao cho OB là đường trung trực của AC. Số đo AOC là
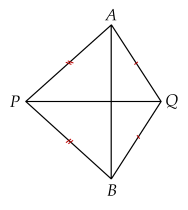
Cho đoạn thẳng AB. Dựng các tam giác PAB cân tại P, tam giác QAB cân tại Q (như hình vẽ).
Hoàn thành khẳng định:
- AB
- PQ
- AB
- PQ
Cho ΔABC có AB<AC. Xác định vị trí của điểm D∈AC sao cho DA+DB=AC.
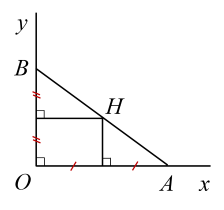
Cho góc vuông xOy. Trên các tia Ox, Oy lần lượt lấy hai điểm A, B (không trùng với O). Đường trung trực của các đoạn thẳng OA và OB cắt nhau ở H. Xét tính đúng, sai của mỗi khẳng định sau.
(Nhấp vào dòng để chọn đúng / sai)| H là trực tâm của tam giác ABO. |
|
| H là trung điểm của AB. |
|
| A, H, B thẳng hàng. |
|
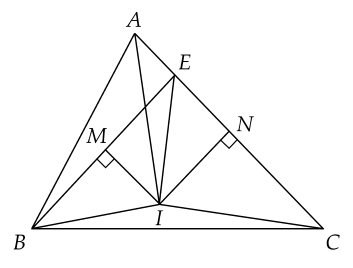
Cho ΔABC có AB<AC, lấy E trên cạnh CA sao cho CE=BA, các đường trung trực của các đoạn thẳng BE và CA cắt nhau ở I. Các khẳng định sau đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| AI là tia phân giác của góc BAC. |
|
| Tam giác IBC cân tại I. |
|
| ΔAIB=ΔAIC. |
|
| ΔAIB=ΔCIE. |
|
Cho góc xOy=α∘, A là một điểm di động nằm trong góc đó. Vẽ các điểm M và N sao cho Ox là đường trung trực của AM, Oy là đường trung trực của AN. Đường trung trực của MN
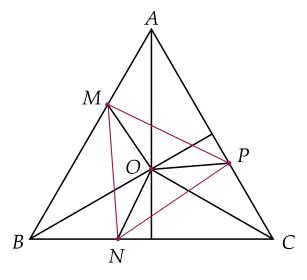
Cho tam giác ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM=BN=CP. Những khẳng định sau đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| BM=CN. |
|
| Tam giác MNP vuông cân tại M. |
|
| Tam giác MNP là tam giác đều. |
|
| AM=AP. |
|

Bạn có thể đăng câu hỏi về bài học này ở đây
