Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Số vô tỉ. Căn bậc hai số học SVIP
I. SỐ VÔ TỈ
1. Khái niệm số vô tỉ
-Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ, những số đó được gọi là số vô tỉ.
-Ví dụ: Số \(\pi\) là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó. Và người ta đã chứng minh được rằng số \(\pi\) số vô tỉ.
2.Số thập phân vô hạn không tuần hoàn
-Khi thực hiện phép chia của \(1\) cho \(3\) ta được kết quả là số thập phân \(0,333...=0,\left(3\right)\), số \(3\) ở phần thập phân lặp mãi. Ta gọi \(3\) là chu kì của số thập phân vô hạn tuần hoàn \(0,\left(3\right)\).
Ngoài ra, ta thấy có vô số chữ số khác \(0\) ở phần thập phân chữ số đó \(\Rightarrow\)Những số thập phân như vậy được gọi là số thập phân vô hạn.
-Tuy nhiên, có những số thập phân vô hạn vô hạn mà ở phần thập phân của nó không có chu kì nào \(\Rightarrow\) Những số như vậy được gọi là số thập phân vô hạn không tuần hoàn.
3. Biểu diễn thập phân của số vô tỉ
Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.
II.CĂN BẬC HAI SỐ HỌC
?Tính: a)\(4^2;\) b)\(\left(0,5\right)^2.\)
Số dương \(4\) thoả mãn \(4^2=16\), ta gọi \(4\) là căn bậc hai số học của \(16\). Tương tự, số dương \(0,5\) thoả mãn \(\left(0,5\right)^2=0,25\), ta gọi \(0,5\) là căn bậc hai số học của \(0,25.\)
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \(x^2=a.\)
|
Chú ý
|
|
Nhận xét: Người ta chứng minh được rằng "Nếu số nguyên dương \(a\) không phải là bình phương của bất kì số nguyên dương nào thì \(\sqrt{a}\) là số vô tỉ". Như vậy các số \(\sqrt{2};\sqrt{3};\sqrt{5};...\) đều là số vô tỉ.
*Tính căn bậc hai số học bằng máy tính cầm tay
Ta có thể sử dụng loại máy tính cầm tay thích hợp để tính căn bậc hai số học của một số không âm. Chẳng hạn:
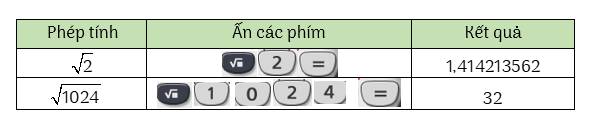

Bạn có thể đánh giá bài học này ở đây