Số nguyên tố. Phân tích số tự nhiên ra thừa số nguyên tố SVIP

1. SỐ NGUYÊN TỐ VÀ HỢP SỐ

Số nguyên tố là số tự nhiên lớn hơn $1$, chỉ có hai ước là $1$ và chính nó.

Hợp số là số tự nhiên lớn hơn $1$, có nhiều hơn hai ước.

 Chú ý:

• Số $0$ và số $1$ không là số nguyên tố và không là hợp số.
• Để khẳng định một số là hợp số, ta thường sử dụng các dấu hiệu chia hết để tìm ra một ước khác $1$ và chính nó.

Ví dụ 1: Số nào dưới đây là số nguyên tố, số nào dưới đây là hợp số? Vì sao?

a) $975$;

b) $23$.

Giải

a) Số $975$ có tận cùng là $5$ nên nó chia hết cho $5$. Do đó, ngoài hai ước là $1$ và $975$ nó còn có thêm ước là $5$.

Vậy $975$ là hợp số.

b) Số $23$ chỉ có hai ước là $1$ và $23$ nên nó là số nguyên tố.

2. PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ

⚡Mọi hợp số đều có thể phân tích được thành tích của các thừa số nguyên tố.

⚡Người ta quy ước dạng phân tích ra thừa số nguyên tố của một số nguyên tố là chính nó.

⚡Khi phân tích một số ra thừa số nguyên tố, trong kết quả ta thường viết các thừa số theo thứ tự từ bé đến lớn và tích các thừa số giống nhau dưới dạng lũy thừa.

Ví dụ 2: 

- Phân tích $12$ ra thừa số nguyên tố được kết quả là $12=2^2.3$.

- Phân tích $15$ ra thừa số nguyên tố được kết quả là $15=3.5$.

 Phương pháp phân tích theo sơ đồ cây

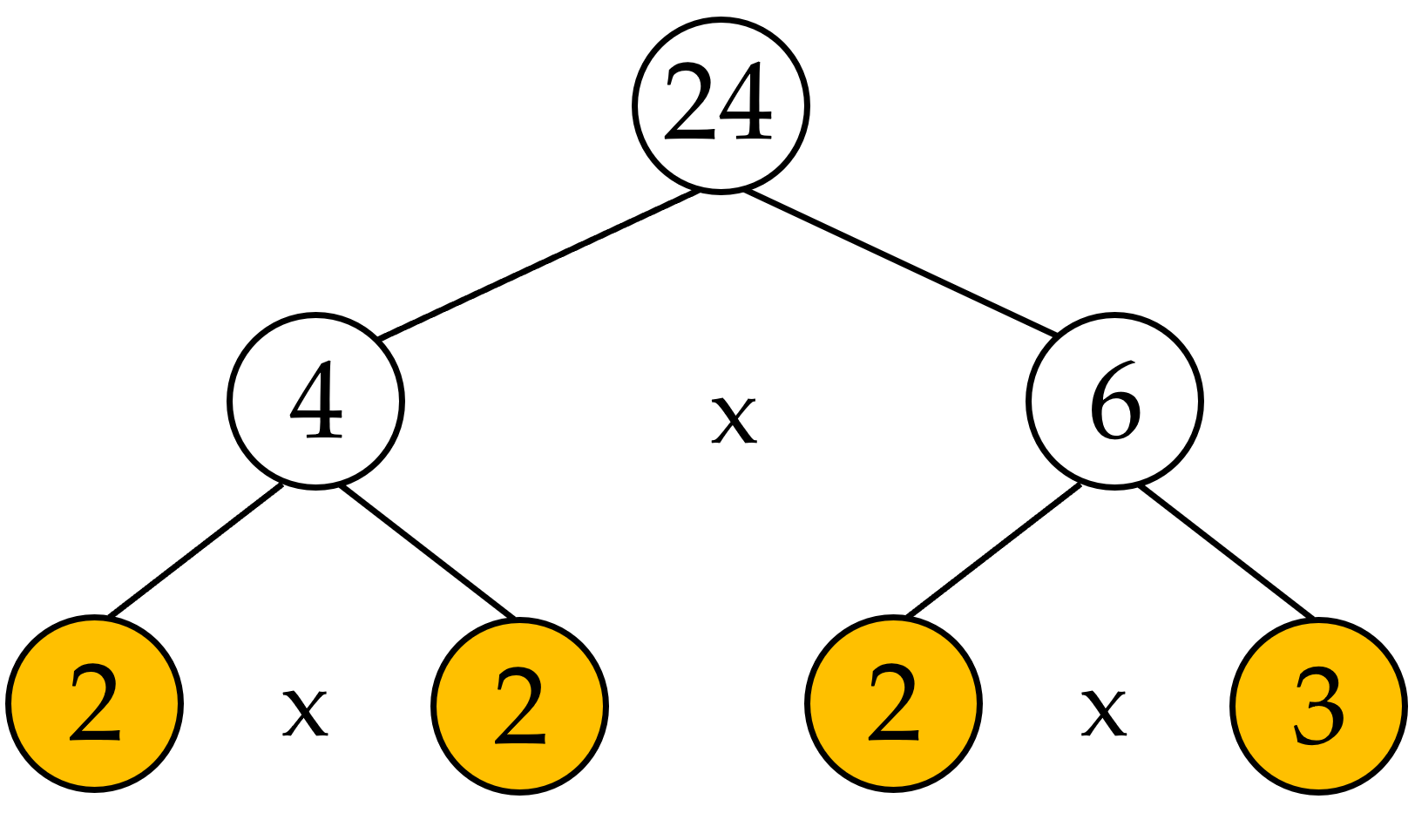
Ta có thể phân tích $24$ thành các số nguyên tố theo sơ đồ cây như sau:

         hoặc 

Vậy $24=2.2.2.3=2^3.3$

Ví dụ 3: Phân tích số $12$ ra thừa số nguyên tố.

Giải

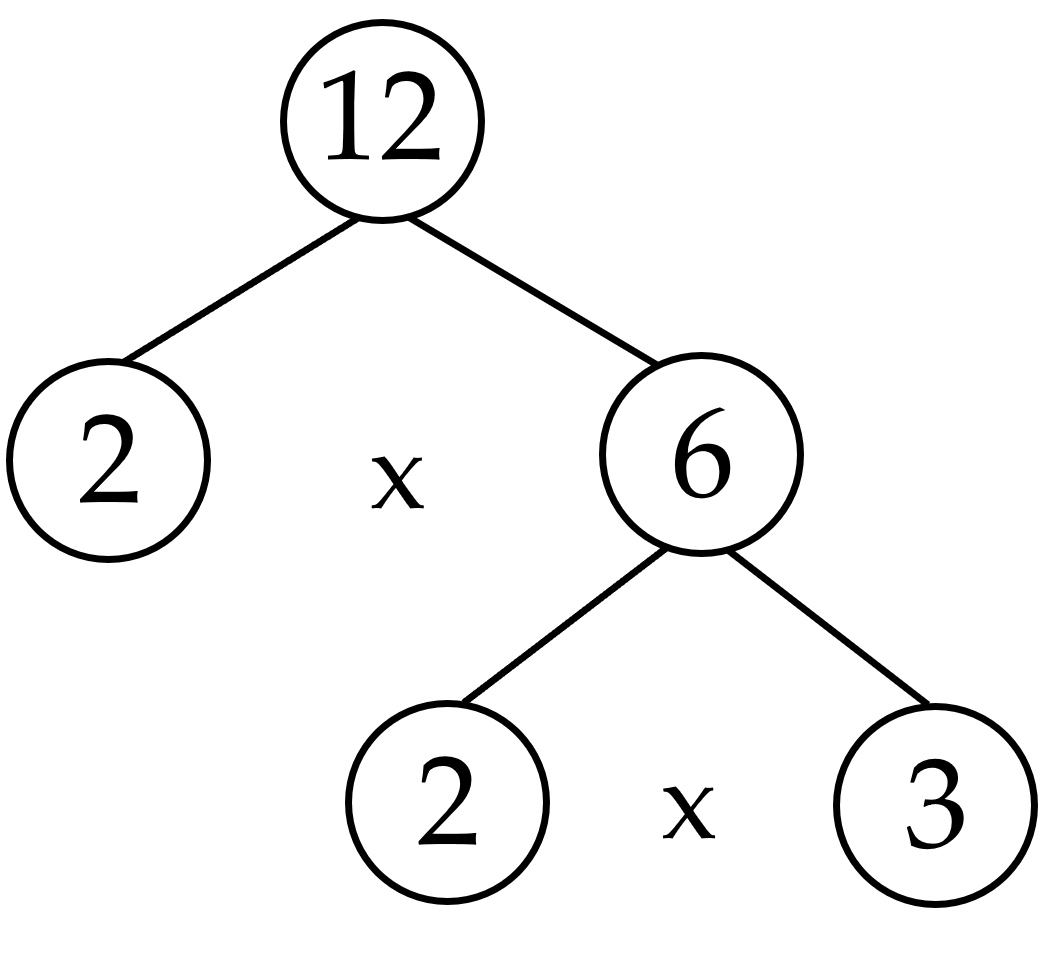
Vậy $12=2.2.3=2^2.3$.

 Phương pháp phân tích theo sơ đồ cột

Ta có thể phân tích $24$ thành các số nguyên tố theo sơ đồ cột như sau:

 Vậy $24=2.2.2.3=2^3.3$

Ví dụ 2: Phân tích số $12$ thành tích các thừa số nguyên tố.

Giải

Vậy $12=2.2.3=2^2.3$.

Nhận xét. Trong hai cách phân tích số $24$ ra thừa số nguyên tố, nếu viết các thừa số nguyên tố theo thứ tự từ bé đến lớn và tích các thừa số nguyên tố giống nhau dưới dạng lũy thừa thì dù phân tích bằng cách nào, ta cũng nhận được cùng một kết quả.