Số nguyên tố. Hợp số SVIP

 KHÁI NIỆM

Số nguyên tố là số tự nhiên lớn hơn $1$, chỉ có hai ước là $1$ và chính nó.

Hợp số là số tự nhiên lớn hơn $1$, có nhiều hơn hai ước.

 Chú ý:

• Số $0$ và số $1$ không là số nguyên tố và không là hợp số.
• Để khẳng định một số là hợp số, ta thường sử dụng các dấu hiệu chia hết để tìm ra một ước khác $1$ và chính nó.

Ví dụ 1: Số nào dưới đây là số nguyên tố, số nào dưới đây là hợp số? Vì sao?

a) $975$;

b) $23$.

Giải

a) Số $975$ có tận cùng là $5$ nên nó chia hết cho $5$. Do đó, ngoài hai ước là $1$ và $975$ nó còn có thêm ước là $5$.

Vậy $975$ là hợp số.

b) Số $23$ chỉ có hai ước là $1$ và $23$ nên nó là số nguyên tố.

Ví dụ 2: 

a) Tìm các ước của $18$.

b) Trong các ước đó, ước nào là số nguyên tố?

Giải

a) Các ước của $18$ là: $1;\, 2;\,3;\, 6;\,9;\,18.$

b) Trong các ước trên, các ước $2$ và $3$ là số nguyên tố.

Chú ý: Nếu số nguyên tố $p$ là ước của số tự nhiên $a$ thì $p$ được gọi là ước nguyên tố của $a$.

Ví dụ 3: Tìm các ước nguyên tố của $51$ và $29$.

Giải

Số $51$ có các ước là: $1;\, 3;\, 17;\,51$, trong đó $3$ và $17$ là số nguyên tố. Vậy các ước nguyên tố của $51$ là $3$ và $17$.

Số $29$ là số nguyên tố. Vậy ước nguyên tố của $29$ là $29$.

 CÓ THỂ EM CHƯA BIẾT

Sàng Ơ-ra-tô-xten (Eratosthenes)

Để tìm các số nguyên tố nhỏ hơn $50$, ta làm như sau:

- Viết tất cả các số tự nhiên từ $2$ đến $50$;

- Khoanh tròn số $2$, gạch tất cả các số là bội của $2$ mà lớn hơn $2$:

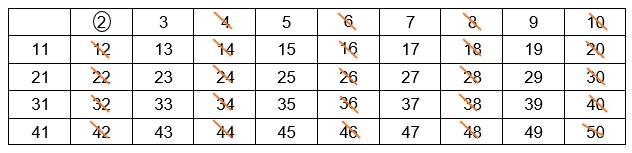
- Khoanh tròn số $3$, gạch tất cả các số là bội của $3$ mà lớn hơn $3$;

- Khoanh tròn số $7$, gạch tất cả các số là bội của $7$ mà lớn hơn $7$;

- Các số không bị gạch trong bảng đều là số nguyên tố.

Các số nguyên tố nhỏ hơn $50$ là: $2;\, 3;\, 5;\, 7;\, 11;\, 13;\, 17;\, 19;\, 23;\, 29;\, 31;\, 37;\, 43;\, 47$.

Số nguyên tố nhỏ nhất là số 2 và đó là số nguyên tố chẵn duy nhất.