olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Phiếu bài tập: Tập hợp và các phép toán trên tập hợp SVIP

In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho tập hợp A={x+1 ∣ x∈NA = \{ x + 1\, \big| \,x \in \mathbb{N}, x≤5}x \le 5\}. Tập hợp AA là

{0;1;2;3;4;5} \{0;1;2;3; 4;5\}.
{0;1;2;3;4;5;6} \{0;1;2;3; 4;5;6\}.
{1;2;3;4;5;6} \{1; 2;3;4;5;6\}.
{1;2;3;4;5}\{1; 2;3; 4;5\}.
Câu 2 (1đ):

Cho tập hợp M={(x;y) ∣ x;y∈NM = \{(x; y)\, \big| \,x; y \in \mathbb{N}, x+y=1}x + y = 1\}. Tập MM có bao nhiêu phần tử?

1.
2.
3.
0.
Câu 3 (1đ):

Tập hợp nào sau đây là tập rỗng?

{x∈Q ∣ x2−4x+2=0}\{x \in \mathbb{Q} \, \big| \, x^2-4x+2=0\}.
{x∈R ∣ x2−4x+3=0}\{x \in \mathbb{R} \, \big| \, x^2-4x+3=0\}.
{x∈Z ∣ ∣x∣<1}\{x \in \mathbb{Z} \, \big| \, |x| < 1\}.
{x∈Z ∣ 6x2−7x+1=0}\{x \in \mathbb{Z} \, \big| \, 6x^2 - 7x + 1=0\}.
Câu 4 (1đ):

Cho tập hợp A={x∈R ∣ (x2–1)(x2+2)=0}A = \{x \in \mathbb{R} \, \big| \, (x^2 –1)( x^2 + 2) = 0\}. Các phần tử của tập AA là

{–2;–1;1;2}\{– 2; –1;1; 2\}.
{1}\{1\}.
{–1}\{–1\}.
{–1;1}\{ –1;1\}.
Câu 5 (1đ):

Tập hợp nào sau đây có đúng một tập hợp con?

{0; x}\{0; \, x\}.
{x}\{ x\}.
{0}\{0\}.
∅\varnothing.
Câu 6 (1đ):

Cho tập hợp A={1;2;5;7}A = \{1; 2;5;7\} và B={1;2;3}B = \{1; 2;3\}. Có tất cả bao nhiêu tập XX thỏa mãn X⊂AX \subset A và X⊂BX \subset B?

22.
66.
88.
44.
Câu 7 (1đ):

Cho tập hợp A={1;2;3;4}A = \{1; 2;3;4\}, B={0;2;4}B = \{0; 2; 4\}, C={0;1;2;3;4;5}C = \{0;1;2;3; 4;5\}. Quan hệ nào sau đây là đúng?

A∪B=CA \cup B = C.
B⊂A⊂CB \subset A \subset C.

{A⊂CB⊂C\left\{ \begin{aligned} &A \subset C\\ &B \subset C\\ \end{aligned} \right..

B⊂A=CB \subset A = C.
Câu 8 (1đ):

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp A={x∈R∣7≤x≤10}A = \{ x \in \mathbb{R} \Big| 7 \le x \le 10\}.

A=(7;10]A = ( 7;10].
A=[7;10)A = [ 7;10 ).
A=(7;10)A = ( 7;10 ).
A=[7;10]A = [7;10 ].
Câu 9 (1đ):

Cho tập hợp: A={x∈R ∣ x−5<4−2x}A = \{ x \in \mathbb{R} \, \big| \, x - 5 < 4 - 2 x\}. Viết lại tập hợp AA dưới kí hiệu khoảng, nửa khoảng, đoạn.

A=(−∞;3)A = ( -\infty; 3 ).
A=(−∞;3]A = ( -\infty;3].
A=[−∞;3)A = [ -\infty;3 ).
A=(3;+∞)A = ( 3; +\infty).
Câu 10 (1đ):

Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp A={x∈R∣∣x∣≤3}A = \{ x \in \mathbb{R} \big| |x| \le 3\} .

A=(−3;3)A = ( -3;3).
A=(−∞;−3]∪[3;+∞)A = ( -\infty; -3] \cup [3; +\infty).
A=[3;+∞)A = [3; +\infty).
A=[−3;3]A = [ -3;3].
Câu 11 (1đ):

Hình vẽ nào sau đây (phần không bị gạch) biểu diễn cho tập A={x∈R∣3x−1≥2}A = \{x \in \mathbb{R} \big| 3x-1\ge 2\}?

loading...
loading...
loading...
loading...
Câu 12 (1đ):

Cho A, B là hai tập hợp bất kì khác tập rỗng được biểu diễn theo biểu đồ Ven sau:

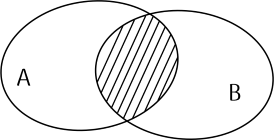
loading...

Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?

B\AB \backslash A.
A∩BA \cap B.
A\BA \backslash B.
A∪BA \cup B.
Câu 13 (1đ):

Lớp 10T2 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10T2 là

10. 
9. 
28.
18. 
Câu 14 (1đ):

Cho tập hợp X={1;5}X = \{1;5\}, Y={1;3;5}Y = \{1;3;5\}. Tập X∩YX \cap Y là 

{1; 3; 5}\{1; \, 3; \, 5\}.
{1}\{1\}.
{1; 3}\{1; \, 3\}.
{1; 5}\{1; \, 5\}.
Câu 15 (1đ):

Cho tập X={0; 1; 2; 3; 4; 5}X = \{0; \,1; \,2; \, 3; \,4; \, 5\} và tập A={0; 2; 4}A = \{0; \, 2; \,4\}. Phần bù của AA trong XX là

∅\varnothing.
{2; 4}\{2; \, 4\}.
{1; 3; 5}\{1; \, 3; \,5\}.
{0; 1; 3}\{0; \,1; \,3\}.
Câu 16 (1đ):

Cho hai tập hợp X={1;2;4;7;9}X = \{1; 2; 4;7;9\} và Y={−1;0;7;10}Y= \{-1;0;7;10\}. Tập hợp X∪YX \cup Y có bao nhiêu phần tử?

77.
99.
1010.
88.
Câu 17 (1đ):

Cho hai tập hợp AA và BB khác rỗng thỏa mãn: A⊂BA \subset B. Mệnh đề nào sau đây sai?

A∪B=BA \cup B = B.
B\A=BB \backslash A = B.
A∩B=AA \cap B = A.
A\B=∅A \backslash B = \varnothing.
Câu 18 (1đ):

Kí hiệu HH là tập hợp các học sinh của lớp 10A. TT là tập hợp các học sinh nam, GG là tập hợp các học sinh nữ của lớp 10A đó. Khẳng định nào sau đây sai?

T∪G=HT \cup G = H.
H\T=GH \backslash T = G.
G\T=∅G \backslash T = \varnothing.
T∩G=∅T \cap G = \varnothing.
Câu 19 (1đ):

Cho tập hợp A=(−∞;−1]A = ( -\infty; -1] và tập B=(−2;+∞)B = ( -2; +\infty ). Khi đó A∪BA \cup B là

(−2;−1]( -2; -1].
∅\varnothing.
(−2;+∞)( -2; +\infty ).
R\mathbb{R}.
Câu 20 (1đ):

Cho hai tập hợp A=[−5;3)A = [ -5;3 ), B=(1;+∞)B = (1; +\infty ). Khi đó A∩BA \cap B là 

(1;3](1;3].
[−5;1][ -5;1].
(1;3)(1;3).
[−5;+∞)[ -5; +\infty ).
Câu 21 (1đ):

Cho hai tập hợp A={x∈R∣(2x−x2)(x−1)=0}A = \{x \in \mathbb{R} \Big|(2 x - x^2 )( x -1) = 0\}, B={n∈N∣0<n2<10}B = \{n \in \mathbb{N} \Big| 0 < n^2 < 10\}. Chọn mệnh đề đúng trong các mệnh đề sau:

A∩B={0;3}A \cap B = \{0;3\}.
A∩B={2}A \cap B = \{2\}.
A∩B={1;2}A \cap B = \{1;2\}.
A∩B={0;1;2;3}A \cap B = \{0;1; 2;3\}.
Câu 22 (1đ):

Cho tập hợp A=[m;m+2]A = [ m; m + 2 ]; B[−1;2]B [ -1; 2 ]. Điều kiện của mm để A⊂BA \subset B là

m≤−1m \le -1 hoặc m≥0m \ge 0.
−1≤m≤0-1 \le m \le 0.
m<1m < 1 hoặc m>2m > 2.
1≤m≤21 \le m \le 2.
Câu 23 (1đ):

Cho hai tập khác rỗng A=(m−1;4]A = ( m - 1; 4]; B=(−2;2m+2)B = ( -2;2m + 2 ) , m∈Rm \in \mathbb{R}. Số thực mm để A∩B≠∅A \cap B \ne \varnothing là

−2<m<5-2 < m < 5.
m>−3m > -3.
1<m<51 < m < 5.
−1<m<5-1 < m < 5.
Câu 24 (1đ):

Cho tập hợp A=(−∞;m−1)A = ( -\infty ; m - 1) và tập B=(2;+∞)B = ( 2; +\infty), giá trị của mm để A∩B=∅A \cap B = \varnothing là

m≤1m \le 1.
m≤3m \le 3.
m>1m > 1.
m<3m < 3.
Câu 25 (1đ):

Cho hai tập hợp A=(m−1;5]A = ( m - 1 ; 5], B=(3;2020−5m)B = (3 ; 2020 - 5m) và AA, BB khác rỗng. Có bao nhiêu giá trị nguyên của mm để A\B=∅A \backslash B = \varnothing?

399399.
22.
33.
398398.
OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP