Bài học cùng chủ đề
- Phép cộng và phép trừ phân thức đại số
- Phép cộng và phép trừ phân thức cùng mẫu
- Phép cộng và phép trừ phân thức khác mẫu
- Tính chất phép cộng phân thức, quy tắc dấu ngoặc
- Phép cộng, trừ phân thức cùng mẫu
- Phép cộng, trừ phân thức khác mẫu
- Quy tắc dấu ngoặc
- Vận dụng tính chất phép cộng phân thức để cộng, trừ nhiều phân thức đại số
- Phép cộng, trừ phân thức đại số theo định dạng đánh giá năng lực🔹
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phép cộng và phép trừ phân thức đại số SVIP
1. CỘNG, TRỪ HAI PHÂN THỨC CÙNG MẪU
+ Quy tắc
Muốn cộng (trừ) hai phân thức có cùng mẫu, ta thực hiện như sau:
- Cộng (trừ) các tử thức với nhau;
- Giữ nguyên mẫu thức.
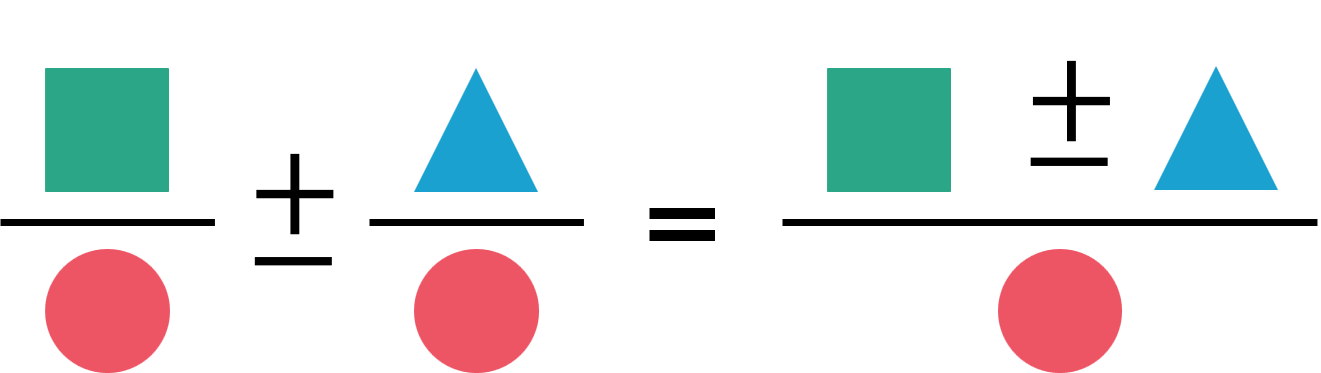
+ Ví dụ 1
$\dfrac AM + \dfrac BM = \dfrac{A + B}M$, với $A, \, B, \, M$ là các đa thức, $M$ khác đa thức $0$;
$\dfrac{a + 2b}3 + \dfrac{2a - b}3 = \dfrac{(a + 2b) + (2a - b)}3$.
+ Ví dụ 2. Thực hiện phép trừ $\dfrac{x^2}{x - 3} - \dfrac{6x - 9}{x - 3}$.
Lời giải
$\dfrac{x^2}{x - 3} - \dfrac{6x - 9}{x - 3} = \dfrac{x^2 - (6x - 9)}{x - 3} = \dfrac{x^2 - 6x + 9}{x - 3} = \dfrac{(x - 3)^2}{x - 3} = x- 3.$
2. CỘNG, TRỪ HAI PHÂN THỨC KHÁC MẪU
+ Quy tắc
Muốn cộng (trừ) hai phân thức khác mẫu, ta thực hiện như sau:
- Quy đồng mẫu thức các phân thức;
Cộng (trừ) các phân thức cùng mẫu vừa tìm được.
+ Ví dụ 3. Thực hiện phép trừ $\dfrac{5}{x} + \dfrac{3}{1 - x}$.
Lời giải
Quy đồng mẫu thức: $\dfrac{5}{x} = \dfrac{5(1-x)}{x(1-x)}$; $\dfrac{3}{1 - x} = \dfrac{3x}{x(1-x)}$.
$\dfrac{5}{x} + \dfrac{3}{1 - x} = \dfrac{5(1-x)}{x(1-x)} + \dfrac{3x}{x(1-x)} = \dfrac{5- 5x + 3x}{x(1-x)} = \dfrac{5-2x}{x(1-x)}$.
3. PHÂN THỨC ĐỐI
Cũng như phân số, mỗi phân thức đều có phân thức đối sao cho tổng của hai phân thức bằng 0.
+ Nhận xét
Phân thức đối của phân thức $\dfrac AB$ kí hiệu là $-\dfrac AB$. Ta có $\dfrac AB + \left(-\dfrac AB\right) = 0$
+ Ví dụ 4:
Phân thức đối của $-\dfrac AB$ là $\dfrac AB$, tức là $-\left(-\dfrac AB\right) = \dfrac AB$;
Phân thức đối của $\dfrac{2x}{-x^2y}$ là $\dfrac{2x}{x^2y}$.
4. TÍNH CHẤT PHÉP CỘNG, TRỪ PHÂN THỨC
Giống như phép cộng phân số, phép cộng phân thức cũng có các tính chất giao hoán, kết hợp và cộng với số 0.
+ Tính chất
Giao hoán: $\dfrac AB + \dfrac CD = \dfrac CD + \dfrac AB$;
Kết hợp: $\left(\dfrac AB + \dfrac CD\right) + \dfrac EG = \dfrac AB + \left(\dfrac CD + \dfrac EG\right)$;
Cộng với $0$: $\dfrac AB + 0 = \dfrac AB$.
+ Ví dụ 5: Rút gọn biểu thức: $Q = \dfrac1x + \dfrac1y - \dfrac1x$
Lời giải
$Q = \dfrac1x + \dfrac1y + \left(- \dfrac1x\right)$ (Thay phép trừ bằng phép cộng với phân thức đối)
$Q = \left[\dfrac1x + \left(- \dfrac1x\right)\right] + \dfrac1y $ (Tính chất giao hoán, kết hợp)
$Q = 0 + \dfrac1y = \dfrac1y $.
+ Chú ý: Trong các biểu thức, ta có thể đổi chỗ các số hạng kèm theo dấu của nó.
$Q = \dfrac1x + \dfrac1y - \dfrac1x = \dfrac1x - \dfrac1x + \dfrac1y = 0 + \dfrac1y = \dfrac1y$.
+ Quy tắc dấu ngoặc:
Nếu trước dấu ngoặc có dấu "+" thì bỏ ngoặc và giữ nguyên các số hạng.
Nếu trước dấu ngoặc có dấu " - " thì bỏ ngoặc và đổi dấu các số hạng trong dấu ngoặc.
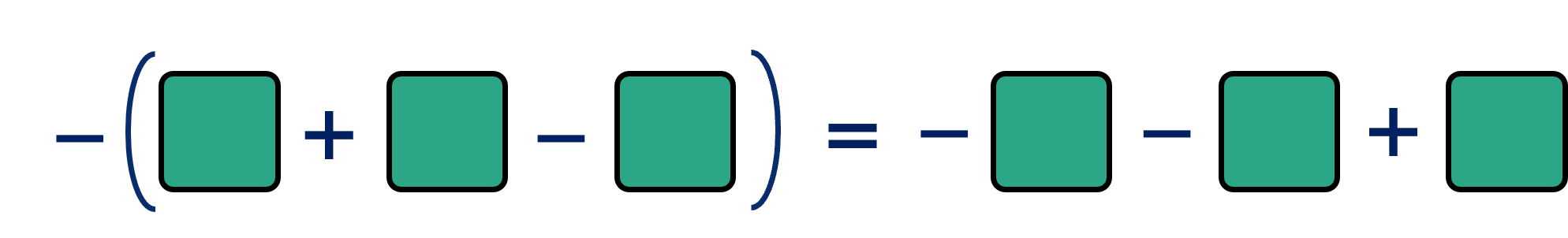

Bạn có thể đánh giá bài học này ở đây